출처 : 소프트웨어 세상을 여는 컴퓨터과학
1. 자료구조의 개요
1) 자료구조의 개념
(1) 데이터 구조 표현
- 대부분의 프로그램은 데이터를 처리해 유용한 정보를 출력한다
- 데이터를 어떤 구조로 표현하느냐에 따라 성능이 달라짐
(2) 자료구조
- 프로그램에서 쉽게 이용할 수 있도록 구성된 데이터 간의 논리적인 관계
- 대표적인 자료구조
ex) 배열, 연결 리스트, 스택, 큐, 그래프, 트리
2. 배열과 연결 리스트
1) 배열
(1) 배열
- 같은 자료형의 데이터를 순서대로 나열한 구조
- 인덱스는 첫 번째로부터 떨어진 상대적인 위치를 나타낸다.
- 배열에서 인덱스의 시작 숫자는 보통 0
(2) 1차원 배열
- 인덱스를 하나만 사용하는 배열
- 1차원 배열에서 임의의 요소 i가 저장된 주소 : base + (i-a)*size
(3) 2차원 배열
- 두 개의 인덱스를 사용하는 배열
- 2차원 배열의 크기를 구하는 공식 : (n-a+1)*(m-b+1)
(a와 b는 행과 열의 인덱스 시작번호 & n과 m은 행과 열 인덱스 마지막 번호)
- 2차원 배열에서 arr[i][j]의 주소를 구하는 공식 (p행 q열)
행 중심 저장 방식 > base + (q*(i-a)+(j-a))*size
열 중심 저장 방식 > base + (p*(j-a)+(i-a))*size
(4) 배열의 특성
- 장점 : 주소를 계산할 수 있으므로 항목 접근 속도가 빠르다
- 단점 :
사용 전에 크기를 지정해야 한다. -> 메모리 낭비 가능성 존재
삽입과 삭제가 어려움
2) 연결 리스트(linked list)
(1) 연결 리스트
- 각 데이터들을 포인터로 연결해 관리하는 구조
- 각 노드들이 주기억장치의 어느 위치에 저장되는지는 상관없다.
- 각 노드들은 포인터로 연결되어 있다.
- 노드가 하나씩 생길 때마다 동적으로 메모리를 할당받기 때문에(malloc()) 메모리 낭비 가능성이 적다.

(2) 단순 연결 리스트(singly linked list)
: 노드에 포인터 영역이 하나인 연결 리스트
- 데이터 삽입

- 데이터 삭제 (데이터가 4인 노드 삭제)

(3) 원형 연결 리스트(circular linked list)
: 마지막 노드의 포인터 영역이 첫 번째노드를 가리키는 연결 리스트 (임의의 노드에서 이전 노드로의 접근이 가능)

(4) 이중 연결 리스트(doubly linked list)
: 각 노드에 다음 노드를 가리키는 포인터 영역과 이전 노드를 가리키는 포인터 영역을 포함한다.

- 데이터 삽입

- 데이터 삭제 (데이터가 4인 노드 삭제)

(5) 이중 원형 연결 리스트
: 이중 연결 리스트의 첫 번째 노드의 이전 노드 포인터 영역이 마지막 노드를 가리키게 하고, 마지막 노드의 다음 포인터 영역이 첫 번째 노드를 가리키도록 구성한 것

3. 스택과 큐
1) 스택(stack)
(1) 스택
- 데이터의 삽입과 삭제가 한쪽 방향에서만 일어나는 구조
- 가장 나중에 삽입된 데이터가 가장 먼저 삭제
- 후입선출(LIFO ; Last-In First-Out)
(2) 배열로 구현한 스택

- 데이터 삽입

- 데이터 삭제

(3) 연결 리스트로 구현한 스택
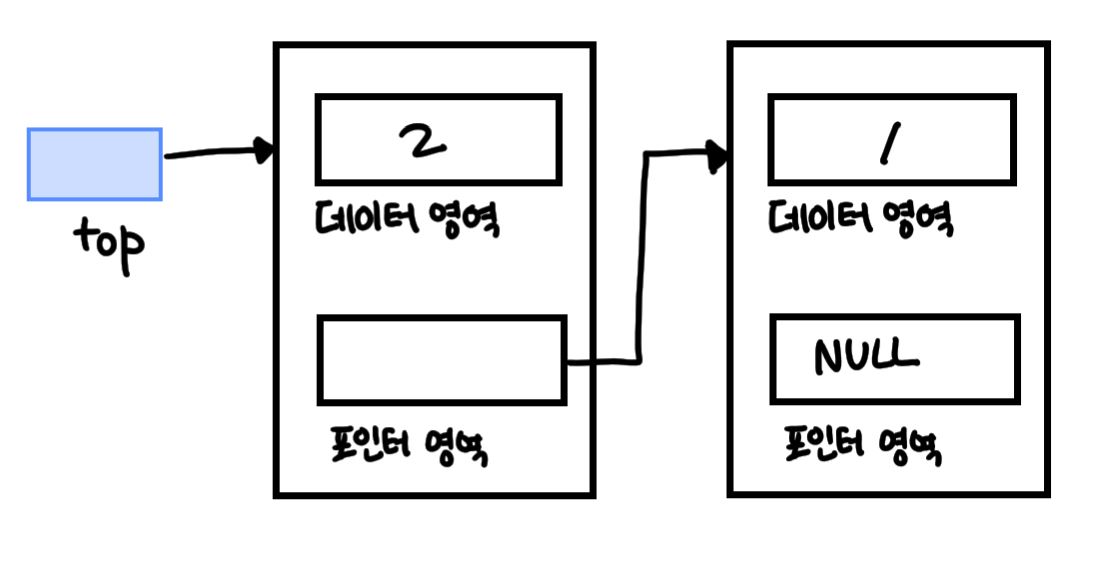
- 데이터 삽입

- 데이터 삭제

(4) 파이썬으로 구현한 스택
stack = []
while True:
select = int(input("1. 삽입 2. 삭제 3. 출력 4. 삭제"))
if select == 1 :
data = int(input("삽입할 데이터 : "))
stack.append(data)
elif select == 2 :
if len(stack) == 0 :
print("스택이 비어 있습니다.")
else :
data = stack.pop()
elif select == 3:
print(stack)
elif select == 4:
print(stack)
print("프로그램을 종료합니다.")
break
else :
print("1~4 사이의 수를 입력하세요. ")
2) 큐(queue)
(1) 큐
- 데이터가 한쪽 방향으로 삽입되고 반대 방향으로 삭제되는 구조
- 가장 먼저 삽입된 데이터가 가장 먼저 삭제
- 선입선출 (FIFO ; First-In First-Out)
(2) 배열로 구현한 큐

- 데이터 삽입

- 데이터 삭제

(3) 원형 큐 ; 배열로 구현한 큐의 문제를 해결
- 큐의 처음과 끝을 연결한 구조

- 데이터 삽입과 삭제

(4) 연결 리스트로 구현한 큐

- 데이터 삽입

- 데이터 삭제

(5) 파이썬으로 구현한 큐
queue = []
while True:
select = int(input("1. 삽입 2. 삭제 3. 출력 4. 종료"))
if select == 1:
data = int(input("삽입할 데이터 : "))
queue.append(data)
elif select == 2:
if len(queue) == 0:
print("큐가 비어 있습니다.")
else :
data = queue.pop(0)
elif select == 3:
print(queue)
elif select == 4:
print("프로그램을 종료합니다.")
break
else :
print("1~4 사이의 수를 입력하세요")
4. 그래프
1) 그래프의 주요 용어
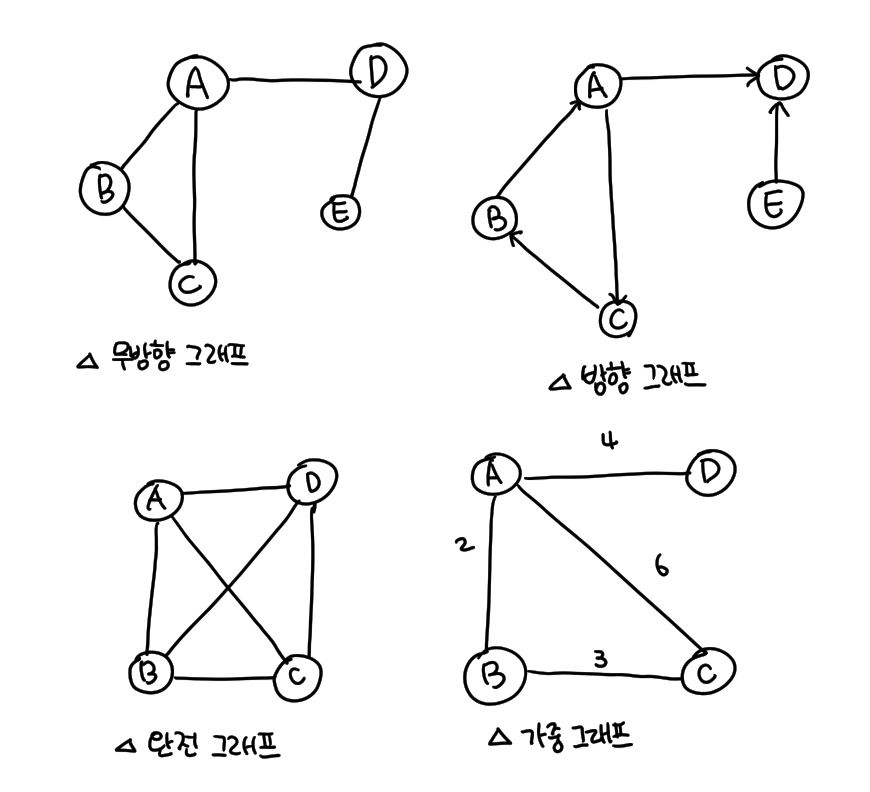
- 정점(node) : 그래프에서 A,B,C,D,E를 지칭
- 간선(edge) : 정점과 정점을 연결하는 선
- 차수(degree) : 정점에 접한 간선의 수
- 그래프 G의 표현 : (정점의 집합, 간선의 집합)으로 표현
- 무방향 그래프 : 방향성이 없는 간선으로 이루어진 그래프
- 방향 그래프 : 방향이 있는 간선으로 이루어진 그래프
- 진입 차수 : 정점으로 들어오는 간선의 수
- 진출 차수 : 정점에서 나가는 간선의 수
- 경로 : 정점에서 다른 정점까지 갈 수 있는 간선들이 있을 때, 간선을 연결하는 정점들을 나열한 것
- 경로의 길이 : 경로에 있는 간선의 수
- 사이클 : 경로 중에서 처음과 마지막 정점이 같은 경로
- 완전 그래프 : 모든 정점 사이에 간선이 있는 그래프
- 가중 그래프 : 간선마다 가중치를 부여한 그래프
2) 오일러의 증명
(1) 쾨니히스베르크의 다리
- 그래프의 시초
- 어떤 지점에서 출발하는지와 상관없이 모든 다리를 한 번씩만 건너서 출발지로 돌아올 수 있는가에 관한 문제
- 수학자 오일러는 이 문제를 해결하기 위해서 쾨니히스베르크의 다리를 그래프로 표현
= > 차수(degree)가 홀수인 정점의 개수가 0일 때만 돌아올 수 있는 경로가 존재함을 증명함.

(2) 오일러 경로(Eulerian path) : 그래프에서 각 연결선을 단 한 번씩만 통과하는 경로
어떤 그래프 G가 오일러 경로를 가지기 위한 필요충분조건은 G가 연결 그래프이고, 홀수 차수의 개수가 0 또는 2인 경우
(3) 오일러 순회(Eulerian circuit) : 그래프에서 꼭짓점은 여러 번 지날 수 있지만, 각 연결선은 단 한 번씩만 통과하는 순회
어떤 그래프 G가 오일러 순회를 가지기 위한 필요충분조건은 G가 연결 그래프이고, 모든 정점들이 짝수 개의 정점을 가지는 경우
3) 그래프의 *탐색
*탐색 : 그래프에서 모든 정점을 방문하는 것
(1) 깊이 우선 탐색(DFS ; Depth First Search)
- 시작 정점에서 시작하여 그 정점과 연결된 방문하지 않은 한 정점을 방문하고, 다음에는 방문한 정점에서 다시 연결된 방문하지 않은 한 정점 순으로 방문함.
- 진행하다가 더 이상 진행할 수 없으면 왔던 길을 되돌아가며 아직 방문하지 않은 정점을 방문
(2) 너비 우선 탐색(BFS ; Breadth First Search)
- 시작 정점을 먼저 방문하고, 시작 정점과 연결된 모든 정점을 방문한다.
- 새롭게 방문한 정점들에 연결된 아직 방문하지 않은 정점들을 방문

5. 트리
1) 트리의 구조와 주요 용어
(1) 트리(tree)
- 링크(link) : 노드와 노드를 연결하는 선
- 루트 노드(root node) : 가장 위에 위치한 노드
- 단말 노드(terminal node) 또는 리프 노드(leaf node) : 트리의 가장 아래에 위치한 노드
- 서브 트리(subtree) : 임의의 아래에 있는 노드들이 다시 트리 구조가 되는 구조
- 부모 노드(parent node) : 임의의 노드 바로 위에 있는 노드
- 자식 노드(child node) : 임의의 노드 바로 아래에 있는 노드
- 형제 노드(sibling node) : 같은 부모 노드를 가지는 노드
- 레벨(level) : 루트 노드에서 임의의 노드까지 방문한 노드의 수
- 깊이(depth) : 트리의 최대 레벨

2) 이진 트리(binary tree)
(1) 이진 트리
- 모든 노드들의 자식 노드가 두 개 이하인 트리
- 왼쪽 서브 트리와 오른쪽 서브 트리로 구분

(2) 완전 이진 트리(complete binary tree)
- 이진 트리 중에서 단말 노드를 제외한 나머지 노드가 모두 두 개의 자식 노드를 가지고 있는 트리

(3) 포화 이진 트리(full binary tree)
- 완전 이진 트리 중에서 모든 노드가 채워진 이진 트리
- 리프 노드가 아닌 노드들은 모두 2개의 자식을 가지고, 모든 리프 노드의 레벨이 동일한 트리

(4) 이진 트리의 표현
- 배열이나 연결 리스트를 이용해 구현 가능
- 주로 연결 리스트를 이용

(5) 이진 트리의 순회
: 이진 트리의 모든 노드를 특정한 순서대로 한 번씩 방문하는 것
- 전위 순회(preorder traversal)
- 중위 순회(inorder traversal)
- 후위 순회(postorder traversal)

3) 이진 탐색 트리(binary search tree)
- 이진 트리 중에서 같은 데이터를 갖는 노드가 없음
- 왼쪽 서브 트리에 있는 모든 데이터가 현재 노드의 데이터보다 작음
- 오른쪽 서브 트리에 있는 모든 데이터가 현재 노드의 데이터보다 큼

- 데이터 삽입

- 데이터 삭제


'전공과목 정리 > IT개론' 카테고리의 다른 글
| [IT개론🗃️] 알고리즘 (2) | 2022.06.24 |
|---|---|
| [IT개론🗃️] 데이터베이스 (0) | 2022.06.22 |
| [IT개론🗃️] 프로그래밍 언어 (0) | 2022.06.21 |
| [IT개론🗃️] 운영체제 (0) | 2022.06.21 |
| [IT개론🗃️] 컴퓨터구조 (0) | 2022.02.14 |