내용 출처 : 소프트웨어 세상을 여는 컴퓨터과학
1. 수의 체계와 변환
1) 수의 체계
(1) 진법 : 사용할 수 있는 숫자의 개수와 각 숫자의 위치값을 정의한 수 체계
(2) 진법의 종류 : 10진법, 2진법, 8진법, 16진법 등
(3) 진법 표현 방법
- 해당 진법을 아래첨자로 표시
- ex) 0.24₂
(4) 자릿값
- 각 숫자의 자릿값은 그 위치가 의미하는 제곱수를 해당 진법에 적용
- ex) 1010₂ = 1*2^3 + 0*2^2 + 1*2^1 + 0*2^0
2) 진수 변환
다른 진수 <-> 10진수
2진수 <-> 2^n진수 (n >= 2)
x진수 <-> p진수
(1) 다른 진수 <-> 10진수
① 8진수 -> 10진수
8진수 27.42 => 10진수 23.53125
방법 : 2*8^1 + 7*8^0 + 4*8^(-1) + 2*8^(-2) = 16 + 7 + 0.5 + 0.03125 = 23.53125
② 10진수 -> 2진수


(2) 2진수 <-> 2^n진수
① 2진수 -> 2^n진수
- 소수점을 기준으로 n만큼 자른 후 잘린 부분의 숫자를 바꾸고자 하는 진법의 수로 변환한다. 빈 공간은 0으로 채우면 된다.

② 2^n진수 -> 2진수


(3) x진수 -> p진수
: x진수 -> 10진수 -> p진수 형태로 변환한다.
2. 정보의 표현
1) 컴퓨터의 정보 표현 방식
(1) 컴퓨터의 정보 표현 방식
- 컴퓨터는 문자, 정수, 실수, 그림, 소리, 동영상 등의 모든 정보를 2진수 형식으로 표현한다.
(2) 비트
- 하나의 0 또는 1
- 컴퓨터에서 정보를 나타내는 최소 단위
- 여덟 개의 비트를 묶으면 1바이트가 된다.
2) 문자 표현
(1) 아스키 코드
- 각 문자를 7비트로 표현
- 최대로 표현할 수 있는 문자 수는 2^7개
(2) 확장 아스키 코드
- 각 문자를 8비트로 표현
- 총 256개의 문자를 표현 가능하다.
(3) 유니코드
- 언어와 상관없이 모든 문자를 16비트로 표현
- 여러 나라의 언어를 표현하고자 만든 코드 체계
- 사용 중인 운영체제, 프로그램, 언어에 관계없이 문자마다 고유한 코드값을 제공
- 최대 2^16개의 문자를 표현할 수 있다.
(4) 허프만 코딩
- 자주 사용되는 문자는 적은 수의 비트로, 자주 사용되지 않는 문자는 많은 수의 비트로 표현
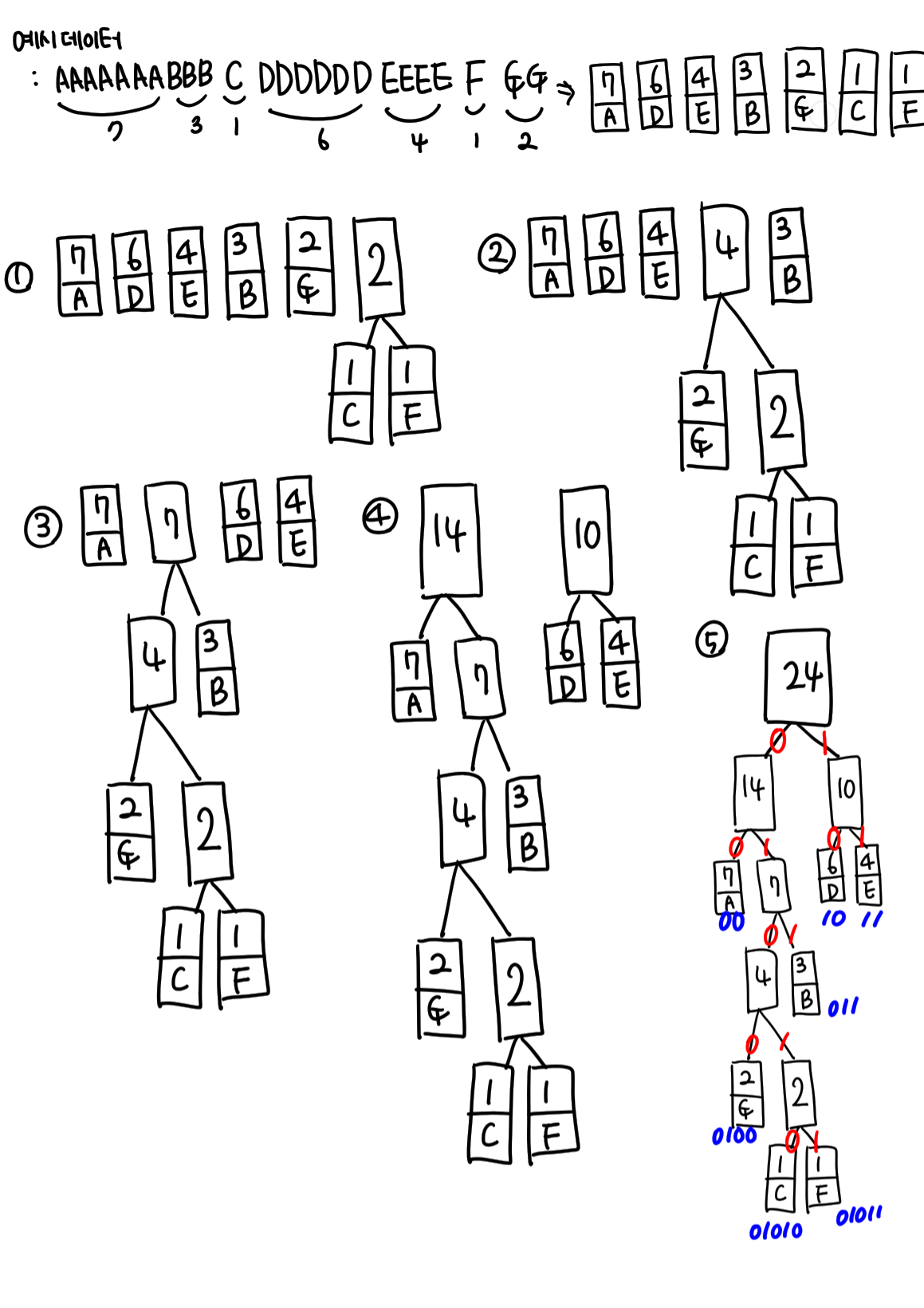
| 문자 | 출현 빈도 | 허프만 코드 | 코드 길이(비트 수) |
| A | 7 | 00 | 2 |
| D | 6 | 10 | 2 |
| E | 4 | 11 | 2 |
| B | 3 | 011 | 3 |
| G | 2 | 0100 | 4 |
| C | 1 | 01010 | 5 |
| F | 1 | 01011 | 5 |
- 허프만 코드의 압축률
A~ G까지 총 7개의 문자가 사용되었으므로 3비트의 고정된 비트수를 배정한다.
7+6+4+3+2+1+1=24
7/24*2 + 6/24*2 + 4/24*2 + 3/24*3 + 2/24*4 + 1/24*5 + 1/24*5 = 2.54
허프만 코드를 사용하지 않았을 때는 모든 문자에 3비트를 배정하지만 허프만 코드를 이용하면 많이 사용되는 문자는 적은 비트를, 적게 사용되는 문자는 많은 비트를 배정한다.
-> 3비트보다 큰 4비트와 5비트 문자가 있지만 2.54 < 3으로 평균 비트는 더 적게 사용되는 것을 알 수 있다.
압축률 = (3-2.54)/3*100 = 15.3%
3) 정수 표현
(1) 정수 표현 방식
- 32비트로 정수를 표현
- 2의 보수 표기법
양수는 가장 왼쪽 비트를 0으로, 나머지 3개의 비트를 이용해 해당 수를 2진수로 표현한다.
음수는 해당 음수의 절댓값을 2의 보수 표기법을 이용해 변환한 후 1은 0으로, 0은 1로 바꾼 후 1을 더한다.
최상위 비트(부호 비트)는 양수일 때 0, 음수일 때 1이다.
n비트로 표현 가능한 수의 범위는 -2^(n-1) ~ 2^(n-1)-1
(2) 정수의 덧셈과 뺄셈

4) 실수 표현
(1) 실수 표현 방식
- 지수 형식
: 실수를 0.7*10^(-4)과 같이 표현하는 것
지수 형식은 가수(mantissa), 밑수(radix), 지수(exponent)의 세 부분으로 이루어진다.
m*r^e
- IEEE754 표준의 실수 표현 방식
단일 정밀도 형식 : 8비트 지수의 4바이트 형식
이중 정밀도 형식 : 11비트 지수의 8바이트 형식
(2) 실수 표현 예시

(3) 실수의 덧셈과 뺄셈
① 피연산자가 0인지 조사한다.
피연산자가 0이면 A±B에서 B가 0이면 A, A가 0이며 덧셈일 경우 B, A가 0이며 뺄셈일 경우 -B가 결과가 된다.
피연산자가 0이 아닐 경우 아래의 순서를 따른다.
② 지수가 같도록 조절한다.
③ 가수의 덧셈, 뺄셈을 한다.
④ 결과를 정규화시킨다.
⑤ 가수의 자리를 조절한다. (생략되는 경우 있음)
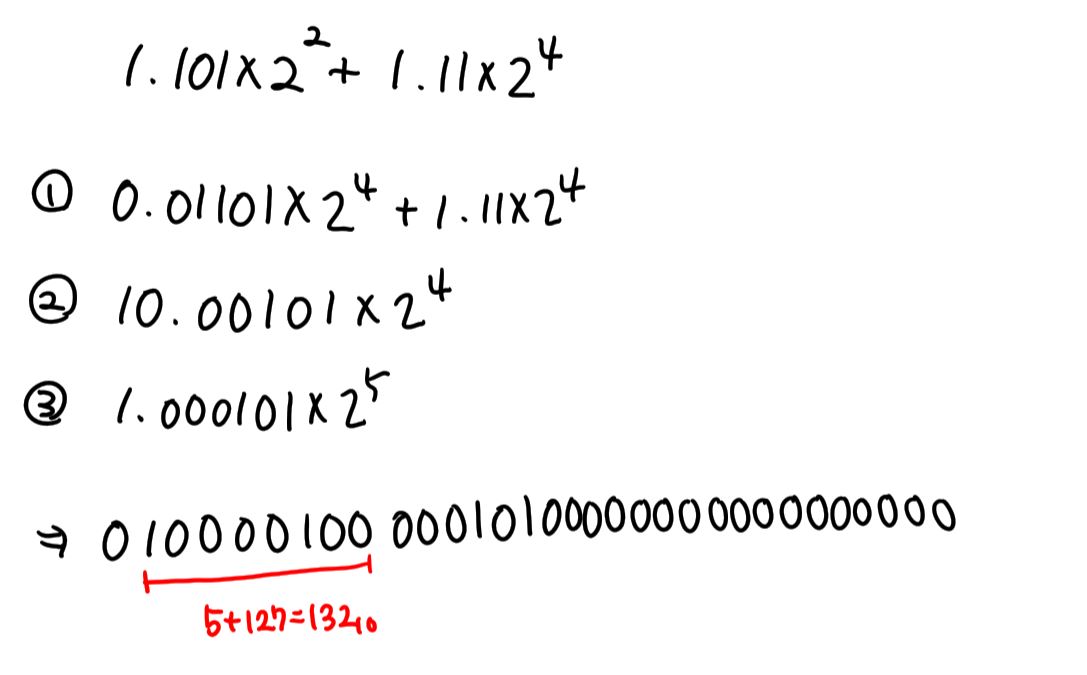

3. 불 대수와 디지털 논리
1) 불 대수 연산
(1) OR연산 ≒ 합집합
연산 결과 두 개의 값 중 하나라도 1이면 1이 되고, 두 개의 값 모두가 0이면 0이 된다.
(2) AND연산 ≒ 교집합
연산 결과 두 개의 값 모두 1이면 1이 되고, 하나라도 0이 있으면 0이 된다.
(3) NOT 연산
연산 결과로 0은 1이 되고, 1은 0이 된다.
2) 불 대수 법칙
- A,B,C가 0 또는 1의 값을 가지는 변수라고 할 때 불 대수와 관련된 법칙
- 교환법칙, 결합법칙, 분배법칙, 드모르간의 법칙이 있다.
ex)
교환법칙 : A+B = B+A , A·B = B·A
결합법칙 : (A+B)+C = A+(B+C) , (A·B)·C = A·(B·C)
분배법칙 : A·(B+C) = (A·B)+(A·C) , A+(B·C) = (A·B)+(A·C)
드모르간의 법칙 : (A+B)' = A'·B' , (A·B) = A' + B'
3) 게이트
(1) OR 게이트
- 불 대수의 OR 연산을 하는 게이트
- 두 개의 입력을 받아 둘 중 하나라도 1이면 1, 둘 다 0이면 0을 출력한다.
(2) AND 게이트
- 불 대수의 AND 연산을 하는 게이트
- 두 개의 입력을 받아 둘 다 1인 경우에만 1, 나머지 경우에는 0을 출력한다.
(3) NOT 게이트
- 불 대수의 NOT 연산을 하는 게이트
- 한 개의 입력만 받아 1이면 0, 0이면 1을 출력한다.
(4) XOR 게이트
- 두 개의 입력을 받아 입력값이 같으면 0 출력, 다르면 1을 출력한다.
(5) NAND 게이트
- AND 게이트 오른쪽에 NOT 게이트를 연결한 것과 같다.
- AND 게이트와 반대로 동작
'전공과목 정리 > IT개론' 카테고리의 다른 글
| [IT개론🗃️] 자료구조 (2) | 2022.06.21 |
|---|---|
| [IT개론🗃️] 프로그래밍 언어 (0) | 2022.06.21 |
| [IT개론🗃️] 운영체제 (0) | 2022.06.21 |
| [IT개론🗃️] 컴퓨터구조 (0) | 2022.02.14 |
| [IT개론🗃️] 컴퓨터과학 도입부 (0) | 2022.01.28 |