[이산수학🔗] 관계 (5장)

포스팅에 참고하는 교재 : 4차 산업혁명 시대의 이산수학 개정판 (생능출판)
IT Cookbook 이산수학

 

5.1 관계와 이항정리

1) 관계(Relation)

- 객체들 간의 연관성을 표현하는 구조로서, 수학이나 공학 분야뿐만 아니라 여러 분야에서도 기본적이고 중요한 개념
- 수학,컴퓨터, 여러 가지 공학 분야에서의 객체들도 이와 같이 여러 가지 관계를 가진다.
- 공학과 수학에 있어서의 관계는 집합에서의 원소들 간의 순서(order)를 고려한 것이다.
- 원소들 간에 '<',  '≤', '≣', '⊂' 등의 관계 연산자를 사용한다.
- 관계의 집합에 대한 연산, 즉 교집합, 합집합, 여집합, 차집합 등도 관계를 가진다.
 

2) 이항 관계 (binary relation)

- 두 집합 A, B에 대하여, A로부터 B로의 이항 관계 R은 두 집합의 곱집합 A×B의 부분 집합이다.
- A×B의 원소인 순서쌍 (a, b)가 주어졌을 때 (a, b) ∊ R 과 aRb는 동치이다.
- 정의에서 사용된 이항(binary)이라는 용어는 2개 집합 사이의 관계를 의미한다.
- 두 개 이상의 원소에 대한 관계는 n-ary 관계라고 한다.
 

3) 관계 R의 원소인 순서쌍

- 첫 번째 원소의 집합을 정의역(domain)이라 하고, Dom(R)로 표시한다.
- 두 번째 원소의 집합을 치역(range)이라고 하고 Ran(R)로 표시한다.
Dom(R) = { a | (a, b) ∊ R } ⊆ A
Ran(R) = { b | (a, b) ∊ R } ⊆ B
 

4) 카티시안 곱(cartesian product) 또는 곱집합

- A와 B가 집합일 때, 순서쌍(ordered pair)의 첫 번째 요소는 집합 A의 원소이고 두 번쨰 요소는 B의 원소로 구성된 모든 순서쌍의 집합을 A와 B의 카티시안 곱(cartesian product) 또는 곱집합이라고 하며 A×B로 나타낸다. 
- A×B = { (x, y) | x∊A, y∊B }
- 카티시안 곱은 두 개 이상의 집합에 대해서도 확장할 수 있다. 
 

5) 역관계(inverse relations)

- 집합 A에서 집합 B로의 관계 R에 대한 역관계 R^-1는 집합 B에서 집합 A로의 관계를 나타내며, 순서쌍 내의 순서를 다시 바꾸면 그 순서쌍은 관계 R에 속하게 된다. 

-  R^-1 = { (b, a) | (a, b) ∊ R }

- aRb의 관계가 있어야 bR^-1a가 가능하다. 

 

5.2 관계의 표현

1) 집합 사이의 관계를 표현하는 방법

(1) 서술식 방법
: "집합 A = {1, 2, 3}에서 원소 a, b가 a ≥ b인 관계 R"과 같이 직접 서술식으로 표현 가능
 
(2) 나열식 방법
- 서술식에 따라 관계를 순서쌍들의 지합으로 표현함.
- 순서쌍의원소들 간의 관계를 표현하는 편리한 방법들로는 화살표 도표(arrow diagram), 좌표 도표(coordinate diagran), 방향 그래프(directed graph), 관계 행렬(relation matrix) 등이 있다. 
 
① 화살표 도표 (Arrow Diagram)

• 화살표 도표를 이용한 관계의 표현은 a가 집합 A의 원소이고, b가 집합 B의 원소라 가정할 때 (a, b)∊R일 경우 집합 A에 있는 원소 a에서 집합 B에 있는 원소 b로 화살표를 그려서 관계를 표현함.

② 좌표 도표 (Coordinate Diagram)

• 관계를 표현하는 방법은 집합 A의 원소를 x축 위의 점으로 표시한다. 
• 집합 B의 원소를 y축 위의 점으로 생각한다. 
• a∊A, b∊B가 관계가 있으면 a를 가리키는 x 좌표축과 b를 가리키는 y 좌표축이 만나는 곳에 점으로 표시한다.

③ 방향 그래프 (Directed Graph)

• 관계 R이 두 집합 A, B 사이의 관계가 아니고 하나의 집합 A에 대한 관계라고 할 때 집합 A의 각 원소를 그래프의 정점(vertex)로 표시한다. (a, b)∊R일 경우 a에서 b로의 화살표가 있는 연결선(edge)인 방향 그래프로 표현한다. 

④ 관계 행렬 (Relation Matrix)

• 관계를 표현하는 또 다른 방법으로서 부울 행렬(Boolean Matrix)을 이용하는 관계 행렬(Relation Matrix) 방법이 있다. 
• 부울 행렬은 행렬 안에 있는 모든 원소들이 0 또는 1로 표시되는 행렬이다. 
• 관계 행렬의 행에는 집합 A의 원소, 열에는 집합 B의 원소를 표시한다. 
• 행렬의 각 요소의 값은 a∊A와 b∊B의 관계가 있으면 1, 관계가 없으면 0으로 표현한다. 

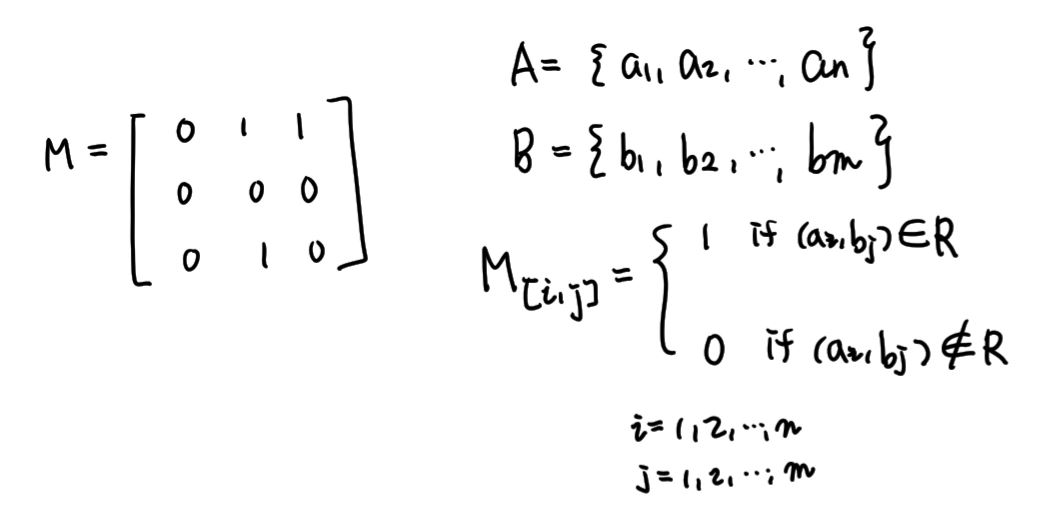
5.3 합성 관계

1) 합성관계

- 세 집합 A, B, C에서 R₁을 집합 A에서 집합 B로의 관계라고 하고, R₂를 집합 B에서 집합 C로의 관계라 하면, 집합 A에서 집합 C로의 합성 관계(composite relation) R₁·R₂ 또는 R₁R₂는 다음과 같이 정의된다.

- R₁·R₂ = {(a,c) | a∊A, c∊C, (a, b)∊R₁이고, (b, c)∊R₂}

- 합성 관계는 주어진 두 관계로부터 새로운 관계를 이끌어내는 것이다.

- 이미 존재하고 있는 관계 R₁과 R2로부터 새로운 관계 R₁·R₂를 만들어냄. 

- 합성관계에서 관계 R₁과 R₂는 연관성이 있어야 하는데, R₁의 치역 안에서 R₂의 정의역이 정의될 경우에만 합성 명제 R₁·R₂를 만들어낼 수 있다. 

 

2) 합성관계의 연산

- R·S은 두 관계행렬 M_R과 M_S의 부울 곱으로 구할 수 있다. 

- 항등관계(identity relation)를 이용한 합성 관계

• 항등관계 : 집합 A에 대한 항등 관계 I_A = {(a, a) | a∊A}
• 항등관계를 이용한 합성 관계는 원래의 관계와 같다. I_AR = RI_B = R

 

5.4 관계의 성질

1) 반사 관계 (Reflexive Relation)

- 관계 R에 대한 방향 그래프를 그렸을 때 그래프의 모든 정점에서 자기 자신을 가라키는 화살표가 있어야 반사관계가 성립한다. 
- 집합 A에 있는 모든 원소 x에 대하여 xRx이면, 즉 (x, x)∊R이면 관계 R을 반사 관계라고 한다. 

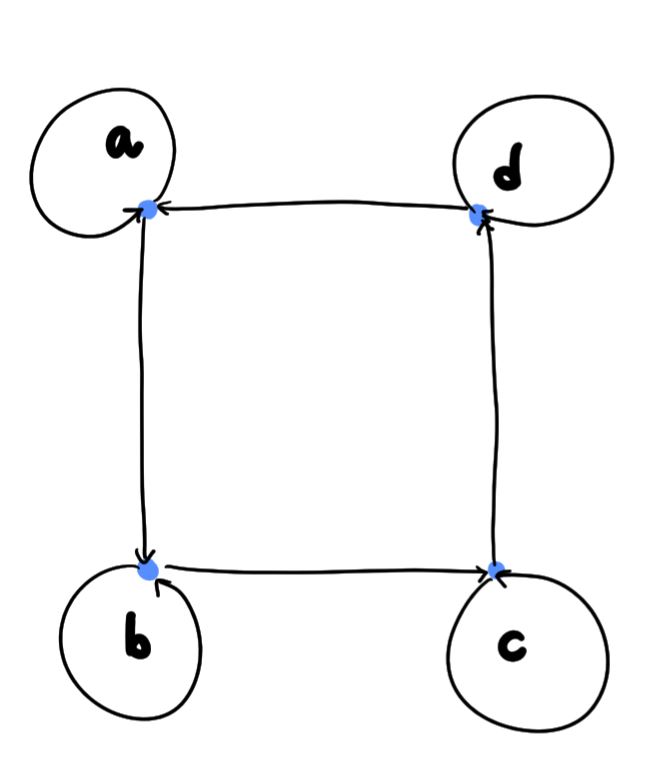
2) 비반사 관계 (irreflexive relation)
- 반사 관계와는 반대로 집합 A의 모든 원소에 대해 a∊A, (a, a)∉R
- R이 비반사 관계이면 R의 원소 중에는 (a, a), a∊A인 원소가 하나도 존재하지 않음.

 
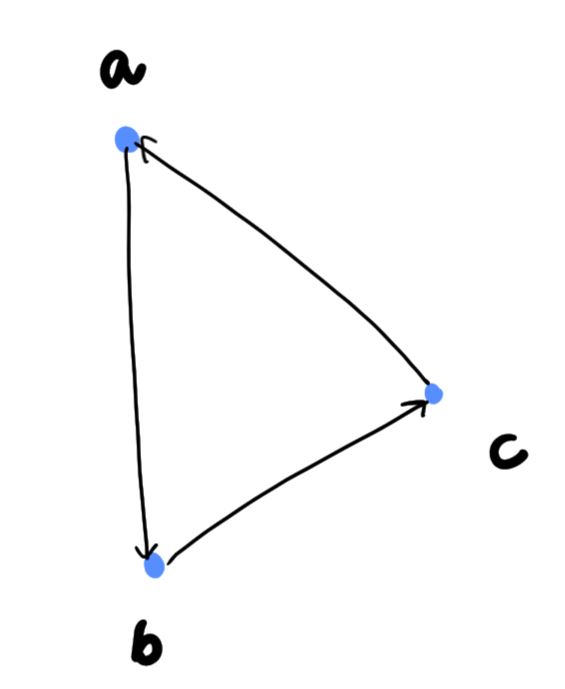
3) 대칭 관계 (symmetric Relation)
- 집합 A에 있는 원소 x, y에 대해 (x, y)∊R일 때 (y, x)∊R이면 관계 R을 대칭 관계라고 한다.
- 대칭 관계인 R을 방향 그래프로 나타내면, 하나의 정점에서 다른 정점으로 화살표가 나가면 반대로 다른 정점에서 그 정점으로의 화살표도 반드시 있어야 함. 

4) 반대칭 관계 (Anti-symmetric Relations) 
- 집합 A에 있는 모든 원소 x, y에 대하여 (x, y)∊R이고, (y, x)∊R일 때 x = y인 관계를 만족하면 관계 R을 반대칭 관계라고 한다. 

 
5) 비대칭 관계 (asymmetric relation)
- 집합 A에 있는 임의의 두 원소  x, y에 대하여 aRb이면 bRa가 아닌 관계
- 반대칭 관계와 비반사 관계를 모두 만족시키는 관계 R
 
6) 추이 관계 (Transitive Relation)
- 집합 A에 있는 원소 x, y, z에 대하여 관계 R이 (x, y)∊R이고, (y, z)∊R이면, (x, z)∊R인 관계를 만족할 때 관계 R을 추이 관계라고 한다. 
- 합성관계의 거듭제곱 ; 추이관계와 거듭제곱의 관계

; 집합 A에 대한 관계 R이 추이관계일 필요충분조건은 모든 양의 정수 n에 대해서 Rⁿ⊆ R이다.

- 추이 클로우저에서는 추이 관계가 성립한다. 

- R의 반사 및 추이 클로우저(reflexive and transitive closure) 
 

 

 - 집합 A에서의 관계 R  ⊆ A × A는 다음과 같은 성질을 가질 수 있다. 

• 반사 관계 : 모든 x ∊ A에 대하여 xRx이다. 
• 대칭 관계 : 모든 x, y ∊ A에 대하여 xRy이면 yRx이다.  
• 추이 관계 : 모든 x, y, z ∊ A에 대하여  xRy이고 yRz이면 xRz이다. 

 

5.5 동치 관계와 분할

1) 동치 관계(equivalence relation)

- 관계 R에서 반사 관계, 대칭 관계, 추이 관계가 모두 성립할 때 이를 동치 관계라고 한다.
- 동치 관계 R의 중요한 성질로는 R이 서로 공통 부분이 없으면서 공집합이 아닌 클래스들로 S를 분할한다는 점이다. 
 

2) 동치류 (equivalence classes) 또는 동치 클래스

- 집합 A에 대한 동치 관계를 R이라고 할 때, A의 각 원소 x에 대하여 [x]를 R에 대한 x의 동치류 또는 동치 클래스라 한다.
- [x] = { y | (x, y) ∊ R } 로 정의한다. 
- 집합 A의 동치류의 모임을 A의 몫집합(quotient set)이라 한다.

 

3) 분할(partitions)

- 공집합이 아닌 집합 A의 분할이란 다음 조건을 만족시키는 A의 부분 집합의 모임을 말한다.

 

 

5.6 부분 순서 관계

1) 부분 순서 관계 (partially ordered relation)

- 집합 A에 대한 관계 R이 반사 관계, 반대칭 관계, 추이 관계이면 관계 R을 부분 순서 관계라고 한다. 

- R이 A에 대한 부분 순서 관계이면 순서쌍 (A, R)을 부분 순서 집합(partially order set, Poset)이라고 한다.

- 부분(patial)이라는 용어를 쓰는 이유는 집합 A의원소의 모든 쌍이 관계를 가지는 것은 아니기 때문이다. 

- 부분 순서 집합을 나타낼 때 (A, ≲)라는 기호를 사용한다. 

- 집합 A에 대한 관계 R이 부분 순서 관계이면, A의 두 원소 x, y에 대하여 (x, y) ∊ R을 x≲y로 표기한다. 

- x≲y의 관계인 경우 'x가 y를 선행한다(x precedes y)' 라고 읽음

 

2) 집합 A에 관한 관계 R이 부분 순서 관계이고 a,b ∊ A일 때

- 비교가능 (comparable) : a≲b 또는 b≲a이면 a와 b는 비교가능

- 비교불가능 (noncomparable) : a≴b이고 b≴a이면 a와 b는 비교 불가능

- 완전순서관계(total order relation) 또는 선형순서관계(linear order relation)

: 집합 A에 속하는 원소들의 모든 쌍이 비교가능할 때의 R

- 완전순서집합(totally ordered set) 또는 선형순서집합(linearly ordered set) : 집합 A

 

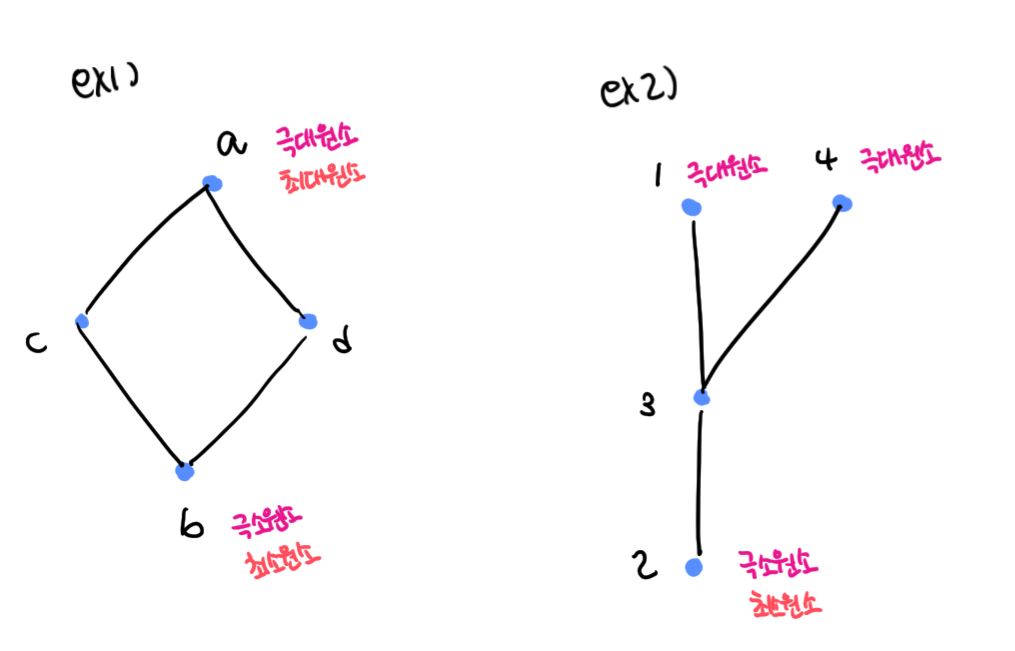
3) 하세 도표 (Hasse Diagram)

- 독일의 수학자 하세(Helmut Hasse, 1898~1979)가 부분 순서 집합  (A, ≲)를 그래프로 나타낼 때 고안하여 사용함. 

- 방향 그래프의 일종으로서 화살표는 표시하지 않고 모든 연결선(edge)을 트리(tree)와 모두 아래 방향을 향하도록 그림

- 모든 순환(loop)은 표시하지 않고 집합 A의 원소 x, y, z에서 x≲y이고 y≲z를 만족하는 y가 존재하지 않을 경우에만 x에서 z로의 연결을 그려준다. 

- 극대원소 (Maximal Element) : 부분순서집합 A의 원소 a에 대해, a≲b인 원소 b가 A에 존재하지 않는 경우 원소 a
- 극소원소 (Minimal Element) : 부분순서집합 A의 원소 a에 대해, b≲a인 원소 b가 A에 존재하지 않는 경우 원소 a
- 최대원소 (Greatest Element) : 부분순서집합 A의 모든 원소 a에 대해  a≲b인 원소 A의 b
- 최소원소 (Least Element) : 부분순서집합 A의 모든 원소 a에 대해 b≲a인 원소 A의 b

4) 관계의 응용과 4차 산업혁명과의 관계

- GPS와 내비게이션에 있어서의 관계의 응용

: GPS(Global Positioning System)는 통상 4개의 인공위성에서 보내는 신호를 수신하여 사용자의 현재 위치를 정확하게 계산하여 알려주는 위성항법 시스템이다. 

- 관계의 다양한 분야에의 응용

: 관계는 순서 관계와 수학, 공학, 함수, 그래프, 트리, 디지털 논리 등에서 매우 중요한 개념으로 응용되고 있다. 

- 관계와 4차 산업혁명과의 관계 : 3D 스캐너와 3D 프린터