포스팅에 참고하는 교재 : 4차 산업혁명 시대의 이산수학 개정판 (생능출판)
7.1 그래프의 기본 개념
1) 그래프 이론
- 18세기 스위스 출신의 저명한 수학자 오일러(Leonhard Euler, 1707~1783)에 의해 그래프 이론이 본격적으로 시작됨.
- 그래프 이론의 대표적인 쾨니히스베르크 다리 문제는 두 개의 섬과 강둑 사이를 연결하는 7개의 다리가 있을 때 각 다리를 꼭 한번씩만 건너는 경로를 찾는 문제
관련 포스팅 : https://0yeonjae2.tistory.com/entry/IT%EA%B0%9C%EB%A1%A0-%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0
[IT개론] 자료구조
출처 : 소프트웨어 세상을 여는 컴퓨터과학 1. 자료구조의 개요 1) 자료구조의 개념 (1) 데이터 구조 표현 - 대부분의 프로그램은 데이터를 처리해 유용한 정보를 출력한다 - 데이터를 어떤 구조로
0yeonjae2.tistory.com
- 그래프(graph) G=(V,E)는 유한한 개수의 정점(vertex) 또는 노드(node)들의 집합인 V와 연결선(edge) 또는 에지라고 불리는 정점들의 쌍들의 집합인 E로 이루어진다.
2) 그래프의 2가지 종류
- 방향 그래프 (directed graph 또는 digraph)
- 방향이 있는 그래프
- 연결선을 화살표로 표시하여 방향을 나타내는 그래프
- v → w인 아크에 대해서 v를 w의 선행자(predecessor)라 하며, w를 v의 후속자(successor)라고 한다.
- 방향이 없는 그래프 (undirected graph)
- 방향이 없는 그래프
- 특별한 언급이 없으면 그래프는 방향이 없는 그래프를 의미한다.
7.2 그래프의 용어
- 경로(path)
- 모든 1≤i<k에 대해서 연결선 (vi, vi+!)이 존재할 때, 정점들의 열(sequence) v1, v2, v3, …, vk라고 한다.
- k≥1이며, 경로의 길이는 k-1이다.
- 단순 경로 (simple path) : 같은 연결선을 두 번 포함하지 않는 경로
- 기본 경로 (elementary path) : 어떤 정점들도 두 번 만나지 않는 경로
- 사이클(cycle) 또는 순회(circuit) : v1 = vk (k≠1)인 경로 == 종점과 시점이 일치
단순 사이클(simple cycle) : 같은 연결선을 반복하여 방문하지 않는 사이클
기본 사이클(elementary cycle) : 시작점을 제외한 어떠한 정점도 반복하여 방문하지 않는 사이클
- 트리 (Tree)
- 사이클(cycle)이 존재하지 않는 그래프
- 루트(root)라고 불리는 특별한 노드가 한 개 존재하고, 루트로부터 다른 모든 노드로 가는 경로가 항상 유일하게 존재한다.
- 루트로 들어오는 연결선이 없으므로 루트는 모든 트리의 출발점이 된다.
- 단순 그래프(single graph)
: 한 쌍의 정점 사이에 많아도 하나의 연결선으로 이루어진, 자기 자신으로의 연결선이 없는 그래프
- 멀티 그래프(multigraph)
: 단순 그래프의 확장으로서 한 쌍의 꼭짓점 사이에 연결선의 개수가 제한이 없는 일반적인 그래프

- 연결선(edge)
- 그래프 G = (V, E)에서 순서화된 쌍 E를 그래프의 연결선이라 한다. (u, v) ∊ E일 때 u와 v를 연결하는 연결선 e는 u와 v에 '접했다(incident)'라 하고 u와 v를 서로 '인접했다'(adjacent)라고 한다.
- 차수(degree)
- G = (V, E)가 그래프이고, u, v가 꼭짓점이라고 할 때 v의 차수(degree) d(v)는 v에 인접하는 연결선의 개수를 말한다.
- 부분그래프(subgraph)
- 두 개의 그래프 G = (V, E), G' = (V', E')에서 V'⊆ V E' ⊆E일 때 그래프 G' = (V', E')를 G의 부분 그래프라고 한다.
- V = V'이고, E'⊂E이면 G'는 G의 생성 부분 그래프(spanning subgraph)이다.

- 연결 그래프(connected graph) : 그래프의 모든 정점들이 연결되어 있는 그래프
- 강한 연결 그래프 (strongly connected graph)
- 그래프에서 모든 두 정점 a, b에 대해서 a에서 b로의 경로와 b에서 a로의 경로들이 존재하는 그래프
- 방향 그래프에서만 의미를 가진다.
- 연결요소 (connectivity component)
- 그래프에서 모든 정점들이 연결되어 있는 부분
- 연결 수(connectivity number) : 그래프 G에서의 연결 요소의 개수
*쾨니히스베르크 다리 문제의 해결 : 멀티 그래프 모델링
- 쾨니히스베리크 다리를 그래프로 나타낸 A, B, C, D로 이름 붙인 점들은 정점을 나타내고, 정점들 사이의 선들을 연결선을 나타냄.
- 멀티 그래프에서 모든 연결선들은 꼭 한 번씩만 통과하는 경로를 오일러 경로(Eulerian path)라고 하는데, 쾨니히스베리크 다리 문제는 오일러 경로를 찾을 수 있는지 여부와 동치이다.
- 멀티 그래프에서 오일러 경로를 판별하는 규칙은 모든 정점에서 그것과 연결된 연결선의 개수가 홀수인 정점(홀수점)의 개수가 0 또는 2개의 경우이다.
- 그래프에서는 A, B, C, D 4개의 정점들이 모두 홀수점을 가지므로 오일러 경로가 없다.
- 따라서 각 다리를 꼭 한 번씩만 건너는 경로는 존재하지 않는다.

- 정점들과 연결선으로 이루어진 도형에 대한 초기의 그래프 이론은 단순하고 직관적인 문제 해결에 국한됨.
- 복잡한 모델에 대한 이론적인 연구로 발전하게 됨.
- 기하학에 위상적인 개념을 접합시킨 응용으로서, 위상 기하학(Topological Geometry)적인 관계를 나타냄.
- 그래프에서 점의 위치나 선의 길이 등에는 특별한 의미를 부여하지 않고 위상적인 형태에만 중점을 둔다.

7.3 그래프의 표현
- 그래프는 그림을 잉요하여 표현하는 것으로 가장 자연스럽고 이해하기도 가장 쉬운 방법이다.
- 컴퓨터는 그림으로 표현된 정보를 이용하는 것이 어렵기 때문에 통상 인접 행렬이나 인접 리스트를 이용해서 표현한다.
- 이를 통해서 컴퓨터 프로그램으로 구현한다.
1) 인접 행렬 (Adjacency Matrix)
그래프 G = (V, E)에서 |V| = n일 때 G의 인접 행렬은 n * n 크기의 행렬 A로 나타나며, A의 각 원소 aij는 다음과 같이 정의된다.

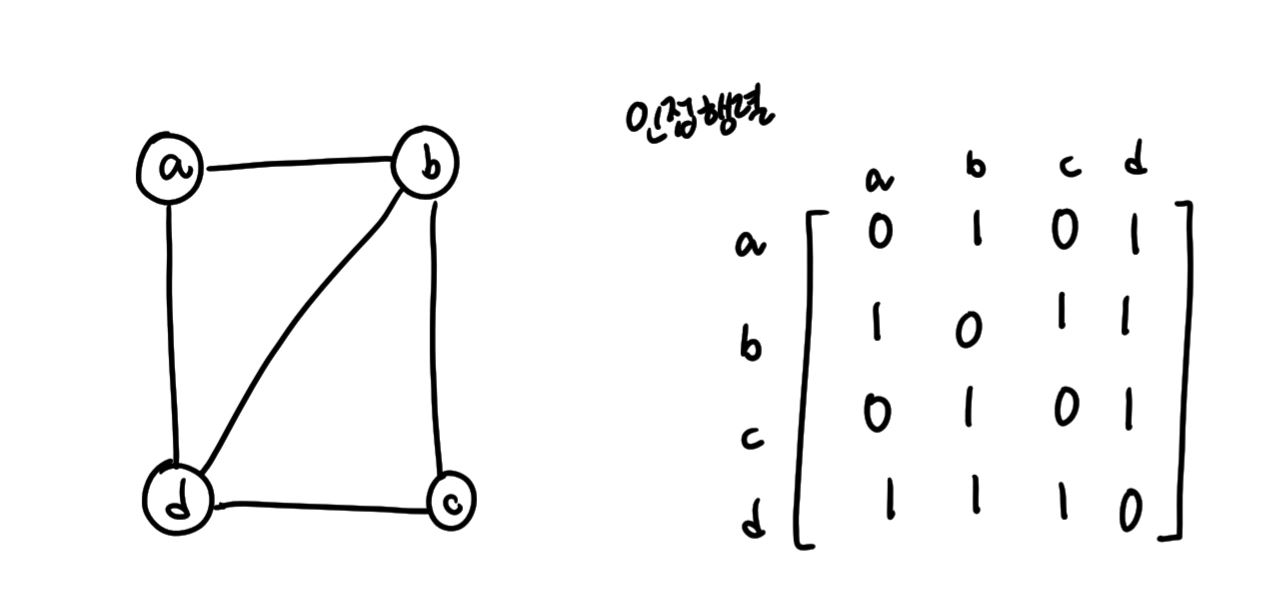
2) 인접 리스트(Adjacency List)

7.4 특수 형태의 그래프
* 차수 : 정점 v와 연결된 연결선의 개수를 정점 v의 차수(degree)라고 하며, deg(v)으로 나타낸다. 이 경우 각 연결선은 그래프의 차수를 계산할 때 두 번 반복해서 계산되므로 그래프에서 모든 정점들의 차수의 합은 연결선들 개수의 2배가 된다.
1) 오일러 경로와 오일러 순회 : 오일러의 성질을 만족하는 특수한 형태의 그래프
(1) 오일러 경로 (Eulerian path) : 그래프에서 각 연결선을 단 한 번씩만 통과하는 경로
- 어떤 그래프 G가 오일러 경로를 가지기 위한 필요충분조건은 G가 연결 그래프이고, 홀수 차수의 개수가 0 또는 2인 경우

(2) 오일러 순회 (Eulerain circuit) : 그래프에서 꼭짓점은 여러 번 지날 수 있지만, 각 연결선을 단 한 번씩만 통과하는 순회
- 어떤 그래프 G가 오일러 순회를 가지기 위해 필요충분조건은 G가 연결 그래프이고, 모든 정점들이 짝수 개의 차수를 가지는 경우
(3) 한붓그리기
- 그래프에서 연필을 떼지 않고 모든 변을 오직 한 번만 지나는 것을 한붓그리기(traversable)라고 한다.
- 연결된 그래프에서 한붓그리기가 가능하려면 시작점과 끝점을 제외한 모든 꼭짓점의 개수가 모두 짝수여야 한다.
2) 해밀턴 경로와 해밀턴 순회 : 해밀턴의 성질을 만족하는 특수한 형태의 그래프
(1) 해밀턴 경로 (Hamiltonian path) : 그래프에서 모든 꼭짓점들을 오직 한 번씩만 지나지만 시작점으로 돌아오지 않는 경로
(2) 해밀턴 순회 (Hamiltonain circuit) : 그래프에서 모든 꼭짓점들을 오직 한 번씩만 지나는 순회

* 경로 : 그래프의 한 꼭짓점에서 이어진 변을 따라 또 다른 꼭짓점으로 이동할 때, 지나간 변을 반복해서 통과하지 않을 경우에 지나온 꼭짓점들을 순서대로 나열한 것
* 순회 : 그래프의 한 꼭짓점에서 출발하여 다시 출발한 꼭짓점으로 돌아오는 경로
3) 가중 그래프 (weight graph)
: 그래프 G의 각 연결선에 0보다 큰 수가 할당되었을 때 이 값을 가중값(weight)이라고 하며, 이와 같은 그래프를 가중 그래프라고 한다.
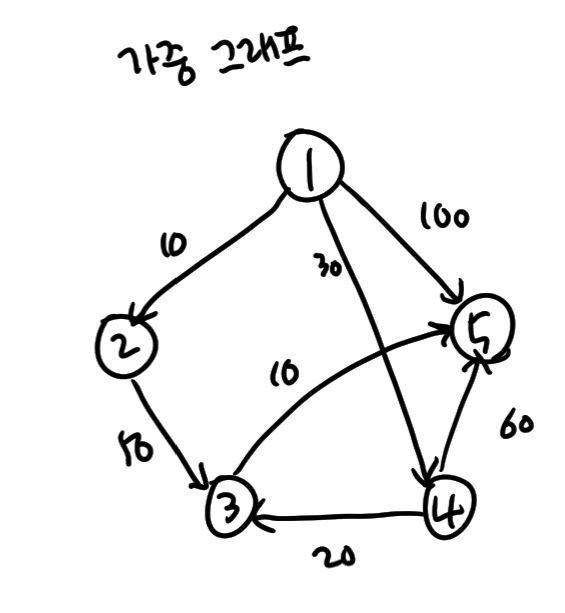
4) 동형 그래프(isomorphic graph)
그래프 G1 = (V1, E1)과 G2 = (V2, E2)가 주어졌을 때, 전단사 함수 f:V1→V2가 존재하여 {u,v}∊E1 ⇔ {f(u), f(v)}∊E2이면 f를 동형(isomorphism)이라고 하고 G1과 G2를 동형 그래프라고 한다.

5) 평면 그래프 (planer graph)
평면상에서 어떠한 연결선들도 서로 교차할 수 없도록 그려진 하나의 그래프
6) 오일러의 정리
연결된 평면그래프에서 꼭짓점의 수를 v, 연결선의 수를 e, 면의 수를 f라고 할 때 v-e+f=2이다.
(평면의 수를 셀 때 그래프 바깥에 있는 평면도 세어야 한다.)

7) 완전 그래프 (complete graph)
- 그래프 G = (V, E)의 모든 정점들의 쌍 사이에 연결선이 존재하면 G를 완전 그래프라고 한다.
- 각 꼭짓점이 다른 모든 꼭짓점들과 연결되는 그래프를 말하는데, n개의 꼭짓점으로 구성된 완전 그래프는 Kn으로 표기
- n개의 정점을 가지는 완전 그래프에서의 연결선의 개수는 n(n-1)/2개이다.

8) k차 정규 그래프
: 그래프 G = (V, E)의 모든 꼭짓점의 차수가 k이면 G를 k차 정규 그래프라고 한다.

9) 이분 그래프 (bipartite graph)
- 그래프 G = (V, E)에서 V가 두 부분 집합 X와 Y=V-X로 나누어져 각 연결선이 X 내의 정점과 Y 내의 정점의 쌍으로 연결되면 그래프 G를 이분 그래프라고 한다.
- 이때 X 내의 모든 정점들과 Y 내의 모든 정점들 사이에 연결선이 존재하면 G를 완전 이분 그래프(complete bipartite graph)라고 한다.
- 이분 그래프는 인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있다.

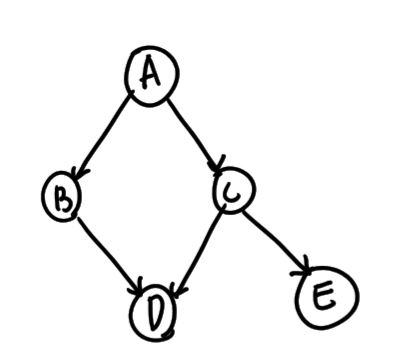
10) 방향 비사이클 그래프 (Directed Acyclic Graph : DAG)
: 사이클이 없는 방향 그래프를 말하는데, 트리보다는 일반적이나 임의의 방향 그래프보다는 제한적이다.
7.5 그래프의 응용
1) 최단 경로
- 그래프는 지도에서 도시를 나타내는 점과 그들 도시 간의 거리를 나타내는 연결선의 값으로 표현된다.
- 도시 A에서 B로 가기 위한 방법
- A에서 B로 가는 경로가 있는가?
- A에서 B로 가는 경로가 여러 개 있을 경우 어떤 경로로 가는 것이 가장 짧은 거리인가?
- 최단 경로 문제 (shortest path problem) : 가장 짧은 거리의 경로를 찾는 문제
- 주어진 방향 그래프에서 경로의 시작점을 출발점(source)이라 하며 목적지를 도착점(destination)이라고 한다.
- 최단 경로의 거리 문제를 해결할 수 있는 방법을 다익스트라 알고리즘(Dijkstr algorithm)이라고 한다.
- 출발점으로부터 거리가 최소로 알려진 점들의 집합 S를 유지함으로써 가장 짧은 거리를 갖는 나머지 점 v를 차례로 S에 포함시킨다.
- 다익스트라 알고리즘
- 주어진 방향 그래프 G = (V, E)에서 v = {1, 2, … , n}이고 점 {1}이 출발점이라고 가정한다.
- 점 i에서 j로 가는 거리를 C[i,j]로 나타내는데, 만약 i에서 j로 가는 경로가 없으면 거리는 ∞가 된다.
- D[i]는 출발점에서 현재점 i에 이르는 가장 짧은 거리를 나타냄
void Dijkstra()
{
S = {1};
for (int i=2; i<=n; i++) D[i] = C[1, i]; // D값 초기화
for (int i=1; i<n; i++)
{
choose a vertax w in V-S such that D[w] is a minimum;
add w to S;
for (each vertex v in V-S) D[v] = min(D[v], D[w] + C[w,v]);
}
}
2) 해밀턴 순회의 응용
- 해밀턴 순회의 응용 문제로는 순회판매원 문제(Traveling salesperson problem)가 있다.
- 순회판매원 문제란 방문해야 할 도시들과 이들 사이의 거리가 주어졌을 경우, 순회판매원이 어떤 특정한 도시를 출발하여 어떠한 도시도 두 번 방문함이 없이 모든 도시들을 거쳐 처음 출발한 도시로 되돌아올 때, 총 여행 거리가 최소가 되는 경로를 찾는 문제이다.
- 최소의 경로가 최적의 경로라고 할 수 있다.
- 일반적인 해결 알고리즘이 존재하지 않는다.
- 최근접 이웃 방법(nearest neighbor method)을 통하여 최솟값은 아니더라도 근사값은 구할 수 있다.
- 임의로 선택한 꼭짓점에서 출발하여 그 꼭짓점과 가장 가까운 꼭짓점을 찾아서 연결하고 있다.
- 경로를 첨가하는 과정을 반복하여 마지막에 순회를 형성하도록 한다.
begin
Choose any v1 ∊ v.
v' ← v1
w ← 0
Add v' to the list of vertices in the path.
while unmarked vertices are remained do
begin
Mark v'
Choose any unmarked vertex, u that is closest to v'.
Add u to the list of vertics in the path.
w ← w + the weight of the edge (v', u)
v' ← u
end
Add v1 to the list of vertices in the path.
w ← w + the weight of the edge {v', v1}
end.
7.6 그래프의 탐색
1) 깊이 우선 탐색 (Depth First Search ; DFS)
- 깊이 우선 탐색은 시작점 v부터 방문한다.
- v에 인접한 정점 중에서 방문하지 않은 정점 w를 방문하고 다시 w부터의 탐색을 시작한다.
- 어떤 정점 u를 방문하고 u에 인접ㅎ한 모든 정점들을 이미 방문한 경우에는 그 전에 마지막으로 방문한 정점으로 되돌아가서 위의 과정들을 반복한다.
- 모든 정점들을 방문한 후에 탐색을 종료한다.
- 순차적인 프로그램보다는 DFS 알고리즘을 재귀(recursive) 알고리즘으로 구현하는 것이 좋다.
- 재귀 알고리즘으로 구현할 경우에는 스택(stack)을 사용한다.
void DFS(int v)
{
int w;
visited[v] = TRUE;
for (each vertex w adjacent to v) if (!visited[w]) dfs(w);
}
/*
G = (V, E)가 n개의 정점을 가진 그래프이고, 처음에는 False 값으로 행렬 visited[n]이 주어졌다고 할 때,
이 알고리즘은 정점 v로부터 도달 가느한 모든 정점들을 방문한다.
*/
2) 너비 우선 탐색
- 너비 우선 탐색은 처음에 방문한 정점과 인접한 정점들을 차례로 방문한다는 점에서 깊이 우선 탐색과 차이가 있다.
- 먼저 시작점 v를 방문한 후에 v에 인접한 모든 정점들을 차례로 방문한다.
- 더 이상 방문할 정점이 없는경우 다시 v에 인접한 정점 가운데 맨 처음으로 방문한 정점과 인접한 정점들을 차례로 방문한다.
- v에 인접한 정점 중 두 번째로 방문한 정점과 인접한 정점들을 차례로 방문하는 과정을 반복한다.
- 모든 정점들을 방문한 후에 탐색을 종료한다.
- 너비 우선탐색은 큐(queue)를 사용한다.
7.7 그래프의 색칠 문제
그래프의 색칠 문제 (coloring problem)
- 어떤 주어진 그래프 G에 대해 인접한 어느 두 영역도 같은 색이 안 되도록 각 정점에 색을 칠하는 문제를 그래프 G의 색칠 문제라고 한다.
- 그래프 G를 색칠하는 데 필요한 최소한의 색의 수를 x(G)로 표현하고 G의 색칠 수(chromatic number)라고 한다.
- 단순 그래프의 색칠은 각각의 정점을 서로 다른 색깔로 색칠함으로써 알 수 있다.
- 대부분의 그래프에서는 정점의 수보다 적은 색깔을 사용해도 색칠이 가능하다.
- 그래프 G에 대해서 다음은 서로 동치이다.
- G는 두 가지 색으로 칠할 수 있다.
- G는 이분 그래프이다.
- G의 모든 순환은 짝수의 길이를 가진다.
- 4색 문제(four coloring problem) : 모든 평면 그래프는 네 가지 색으로 색칠이 가능하다.
7.8 그래프의 응용과 4차 산업혁명과의 관계
1) 모델링과 다양한 학문 분야에서의 응용
: 그래프는 주어진 문제를 모델화하는 데 유용한 도구로써 그 사용이 증가하고 있으며, 최근에는 기하학과 그래픽 등 광범위한 범위에서 응용되고 있다.
2) 컴퓨터 관련 분야에서의 응용
: 그래프 이론은 컴퓨터 관련 분야에 필수적이다. 주요 응용 예로는 논리 회로의 설계 및 분석, 시스템의 흐름도, 컴파일러에서의 최적화 등이 있다.
3) 그래프와 4차 산업혁명과의 관계 : 사물인터넷(Internet of Things : IOT)
: 4차 산업혁명의 한 기술 분야인 사물인터넷은 네트워크 연결이 중심이 되므로 그래프와 관련이 깊다.
'전공과목 정리 > 이산수학' 카테고리의 다른 글
| [이산수학🔗] 순열, 이산적 확률, 재귀적 관계 (9장) (0) | 2023.01.13 |
|---|---|
| [이산수학🔗] 트리 (8장) (2) | 2023.01.13 |
| [이산수학🔗] 함수 (6장) (0) | 2023.01.07 |
| [이산수학🔗] 관계 (5장) (2) | 2023.01.07 |
| [이산수학🔗] 증명법 (4장) (0) | 2023.01.04 |