포스팅에 참고하는 교재 : 4차 산업혁명 시대의 이산수학 개정판 (생능출판)
9.1 경우의 수
1) 경우의 수
- 어떤 사건이 일어나는 경우의 수를 구할 때는 모든 경우를 일정한 기준에 따라 빠짐 없이, 중복 없이 구해야 한다.
- 경우의 수를 구하는 방법에는 트리를 이용하는 방법과 표를 이용하는 방법이 있다.
2) 경우의 수에서의 법칙
- 합의 법칙 (rule of sum)
- 두 사건 A, B (A∩B=∅)가 일어날 경우의 수를 n(A)=m, n(B)=n이라 하면, A 또는 B가 일어날 경우의 수는 m+n이다.
- n(A∪B)=n(A) + n(B) = m+n
- 곱의 법칙 (rule of product)
- 두 사건 A, B에서 n(A)=m, n(B)=n이라 하면, A와 B가 동시에 일어날 경우의 수는 m∙n이다.
- n(A×B) = n(A)×n(B)=m∙n
9.2 수열
1) 순열 (premutation)
- 서로 다른 원소들을 순서를 고려해서 일렬로 배열하는 것
- 서로 다른 n개의 원소를 한 줄로 배열하는 순열의 수 = n!
2) 서로 다른 n개의 원소 중에서 r개를 택하는 순열의 수
- n × (n-1) × ... × (n-r+1) (단, 0<r≤n)
- nPr로 나타낸다
- nPr = n! / (n-r)!
- nPn = n!
- nP0 =1
3) 같은 것을 포함하는 순열
- n개 중에서 같은 것이 각각 p개, q개, ... , r개씩 있을 때, n개를 일렬로 배열하여 만들 수 있는 순열
- n! / (p!q!...r!) (단, p+q+...+r=n)
9.3 조합
1) 조합 (combination)
- 서로 다른 n개의 원소 중에서 순서를 생각하지 않고 r개를 택할 때, 이를 n개의 원소에서 r개를 택하는 조합이라고 한다.
- nCr = nPr/r! = n!/(r!(n-r)!) (단, 0<r≤n)
- C(n,r) , Cn,r 기호를 사용하기도 한다.
2) 이항 정리(binomial theorem)와 이항 계수(binomial coefficient)
(a+b)^n을 전개하면 다음과 같은 식이 나오는데, 이것을 이항 정리라 하고, 이때 nCr를 이항 계수라 한다.
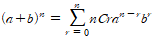
3) 파스칼의 삼각형
- n-1Cr-1 + n-1Cr = nCr
- 이항 계수가 위와 같이 만들어진다.
- 각 행에 있는 첫 번째 숫자와 마지막 숫자는 1이다.
- 삼각형 안의 다른 숫자들을 파스칼의 삼각형과 같이 모두 그 숫자 위로부터 연결된 두 수들을 더함으로써 구할 수 있다.
9.4 이산적 확률과 통계
1) 확률
- 확률 : 어떤 사건 A가 일어날 가능성을 수로 나타낸 것
- 사건 A가 나타날 경우의 수를 전체 경우의 수로 나눈 값이다.
- 확률의 기본 법칙
- 어떤 사건 A에 대하여 0≤P(A)≤1
- 전사건 S의 확률 P(S) = 1
- 공사건 ∅의 확률 p(∅) = 0
- 사건 A가 일어날 확률과 사건 A의 여사건 Ac가 일어날 확률 사이의 관계 : P(A) + P(Ac) = 1, P(Ac) = 1 - P(A)
2) 확률 변수와 이산적 확률(discrete probability)
- 확률 변수 : 변수 X가 취할 수 있는 모든 값이 x1, x2, x3, ... xn이고, X가 이들 값을 취할 확률 p1, p2, p3, ... pn이 정해져 있을 때의 변수 X
- 이산적 확률 : 확률 변수 X가 이산적인 값을 취할 때의 확률
- 확률분포 : 확률 변수 X가 취하는 값 xi와 X가 xi를 취할 확률 pi와의 대응 관계
- X의 기대값 또는 평균

- X의 분산(variance)
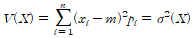
- X의 표준 편차(standard deviation)
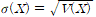
3) 베이즈의 정리(Bayesian theorem)
- 표본 공간이 n에서 서로 다른 배반적인 사건 B1, B2, ..., Bn중 하나는 반드시 일어난다고 할 때, 임의 사건 A에 대하여 아래의 식이 성립한다.
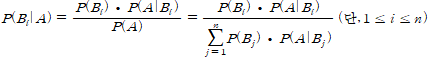
- 조건부 확률 (Conditional Probabilty)
- 추가적인 정보나 증거(evidence)가 주어졌을 때 어떤 명제나 사건이 발생할 확률
- P(A|B) = P(A,B)/P(B) : 증거 B가 주어졌을 때 사건 A가 발생할 확률
- P(A,B) = P(A|B)P(B) : 조건부확률과 결합확률
- 베이스 규칙 (Bayes' Rule)
- P(X|Y) = P(X,Y)/P(Y), P(Y|X) = P(Y,X)/P(X) = P(X, Y)/P(X)
- 위 식의 양변에 각각 P(X), P(Y)를 곱한 후 각각의 결과를 등식으로 연결하면 아래와 같다.
- P(X|Y) = P(Y|X)P(X)/P(Y)
9.5 비둘기 집 원리
1) 비둘기 집 원리
n개의 비둘기 집에 (n+1)마리 이상의 비둘기가 들어갔다면, 두 마리 이상의 비둘기가 들어간 비둘기집이 적어도 하나 있다.
2) 비둘기 집 원리 예시
ex) m개의 정수 a1, a2, ... , an이 주어져 있다. 이 중 연속된 항의 합은 m의 배수가 됨을 보여라.

9.6 재귀적 정의
1) 재귀적 관계식
- 재귀적 정의(recursive defination) : 수학적 귀납법에서와 같이 첫 번째 요소가 정의되고, n+1 번째 요소는 바로 앞의 n번쨰와 그 이하의 요소와의 관계로서 정의될 경우를 말하며, 재귀적 관계(recurrence relation)로 표현된다.
2) 재귀적 관계의 예시
- 프랙탈 (Fractals)
- 물리학에서의 동역학계와 카오스(Chaos)를 비롯한 지능 시스템 분야에서 많이 활용되고 있다.
- factorial
int fact(int n)
{
if (n<=1) return 1;
else return n*fact(n-1);
}9.7. 피보나치 수와 하노이 탑
1) 피보나치 수 (Fibonacci numbers)
- 다음과 같은 재귀적 관계식으로 정의된다.
- fibo(0) =0, fibo(1) = 1
- fibo(n) = fibo(n-1)+fibo(n-2) (n≥2)
int fibo(int n)
{
if (n == 0) return 0;
else if (n == 1) return 1;
else return fibo(n-1)+fibo(n-2);
}
2) 하노이 탑(Tower of Hanoi)
- 각가 다른 크기의 원반들과 판 위에 세워진 세 개의 막대로 구성된다.
- 이 원반들은 처음에 바닥에 가장 큰 원반이 있는 크기 순으로 놓인다.
- 하노이 탑 문제의 규칙은 원반들이 한 막대에서 다른 막대로 한 번에 하나씩 이동할 수 있으며 작은 원반위에 큰 것이 놓일 수 없도록 하는 것이다.
- 중간의 막대를 임시적으로 이용할 수 있으나 위의 규칙들을 지켜야 한다.
void hanoi(int n, char from, char tmp, char to)
{
if (n == 1) printf("원반 1을 %c에서 %c로 옮긴다.\n", from, to);
else
{
hanoi(n-1, from, to, tmp);
printf("원반 %d를 %c에서 %c로 옮긴다.\n", n, from, to);
honoi(n-1, tmp, from, to);
}
}
* 관련 포스팅
https://0yeonjae2.tistory.com/entry/IT%EA%B0%9C%EB%A1%A0-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
[IT개론] 알고리즘
출처 : 소프트웨어 세상을 여는 컴퓨터과학 1. 알고리즘의 개요 1) 알고리즘의 개념 (1) 알고리즘(algorithm) - 어떤 문제를 해결하기 위해 구성된 일련의 절차 (2) 알고리즘의 조건 - 0개 이상의 입력,
0yeonjae2.tistory.com
9.8 순열, 이산적 확률, 재귀적 관계의 응용과 4차 산업혁명과의 관계
1) 베이즈의 정리를 이용한 미래 예측
: 과거의 데이터를 기반으로 미래를 예측하는 모델인 베이즈의 정리는 기상 예측, 의료 분야의 질병 예측, 게임의 승부 예측 등에 널리 응용된다. 또한 확률 모델을 활용한 음성 인식 기술도 개발되고 있다.
2) 컴퓨터 프로그램에서의 재귀함수
: 재귀적 관계식은 정수의 계승(factorial), 피보나치 수, 하노이 탑 등의 정의에 적용된다. 재귀함수를 잘 이용하면 복잡한 알고리즘을 매우 간단하게 표현할 수 있다.
3) 이산적 확률과 4차 산업혁명과이 관계 : 빅 데이터
- 빅 데이터(Big data)란 기존의 데이터베이스 관리 능력을 뛰어넘는 엄청난 양의 정형 또는 비정형 데이터들로부터 가치를 추출하고 결과를 분석하는 4차 산업혁명이 한 기술 분야이다.
- 빅데이터는 확률을 비롯한 기존의 통계적 분석 기법에 대규모 데이터를 접목시켜 4차 산업혁명에서 촉망받는 응용 분야로 부각되고 있다.
'전공과목 정리 > 이산수학' 카테고리의 다른 글
| [이산수학🔗] 부울 대수 (11장) (0) | 2023.01.18 |
|---|---|
| [이산수학🔗] 행렬과 행렬식 (10장) (2) | 2023.01.15 |
| [이산수학🔗] 트리 (8장) (2) | 2023.01.13 |
| [이산수학🔗] 그래프 (7장) (0) | 2023.01.13 |
| [이산수학🔗] 함수 (6장) (0) | 2023.01.07 |