포스팅에 참고하는 교재 : 4차 산업혁명 시대의 이산수학 개정판 (생능출판)
11.0 부울 대수 (Boolean algebra)
- 1854년 영국의 수학자 부울(George Boole, 1825~1864)이 쓴 《사고의 법칙 연구(An Investigation of the Laws of Thought)》에서 수학적 논리 형태로 처음 소개되었다.
- 1938년 섀넌(Shannon)이 부울 대수의 기본 개념을 이용하여 회로 함수에 대한 설계로 발전시킨다.
- 0과 1의 조합으로 연산되는 것을 부울 대수라고 한다.
- 전기 장치나 컴퓨터 회로는 켜짐과 꺼짐의 두 가지 상태로 나타낸다.
- 스위치나 회로는 닫힘과 열림의 두 가지 상태 중 하나의 참 또는 거짓, 1 또는 0으로 표현될 수 있다.
11.1 부울식
1) 부울식
- 두 원소를 가지는 집합 A = {0, 1}과 이항 연산자(binary operator) +(OR)과 ·(AND), 그리고 단항 연산자(unary operator) '(complement)로 표현되는 식을 말한다.
- 연산자의 우선순위 : ' > · > +
- 부울식의 정의
- 상수 0과 1 그리고 부울 변수는 부울식이다.
- f1, f2가 부울식일 때 f1', f1+f2, f1·f2 역시 부울 이다.
- 부울식에서 부울 변수가 가질 수 있는 값인 0 또는 1을 정해줌으로써 각 부울식에 대한 값을 구할 수 있다.
- 두 부울식이 같은 진리표(truth table)를 가질 경우 두 부울식을 동치(equivalent)라고 한다.
- 두 함수 f1과 f2가 동치인 경우 f1=f2 로 표시한다.
2) 부울식의 법칙
- p, q ,r을 부울 변수라 한다.
- 멱등 법칙 (idempotent law) : p·p=p, p+p=p
- 항등 법칙 (identity law) : p+0=p, p·1=p
- 교환 법칙 (commutative law) : p+q=q+p, p·q=q·p
- 결합 법칙 (associative law) : p+(q+r)=(p+q)+r, p·(q·r)=(p·q)·r
- 분배 법칙 (distributive law) : p+(q·r)=(p+q)·(p+r), p·(q+r) = (p·q)+(p+r)
- 흡수 법칙 (absorption law) : p+(p·q)=p, p·(p+q)=p
- 역 법칙 (inverse law) : p+p'=1, p·p'=0
- 보 법칙 (complement law) : (p')'=p
- 우등 법칙 (dominance law): p+1=1, p·0=0
- 드 모르간의 법칙 (De Morgan's law) : (p+q)'=p'·q', (p·q)' = p'+q'
11.2 부울식의 표현
1) 부울 함수 (Boolean function)
- 부울 변수들에 대한 함수
- n개의 부울 변수에 대한 부울 함수는 f(x1, ..., xn)으로 표시한다.
- 부울 변수와 부울 연산자로 구성된 부울식으로 표현할 수 있다.
- n개의 부울 변수가 있을 때 그 변수들로부터 얻을 수 있는 조합은 2n개이다.
- 0은 그에 해당되는 원소가 없는 경우이고, 1은 있는 경우이다.
- n개의 부울 변수로 만들어지는 진리표에서 변수의 각 항을 최소항(Minterm)이라고 한다.
- n개의 변수가 있으면 2n개의 최소항이 있게 된다. 각 최소항들은 n개의 부울 변수들의 곱으로 나타낸다.
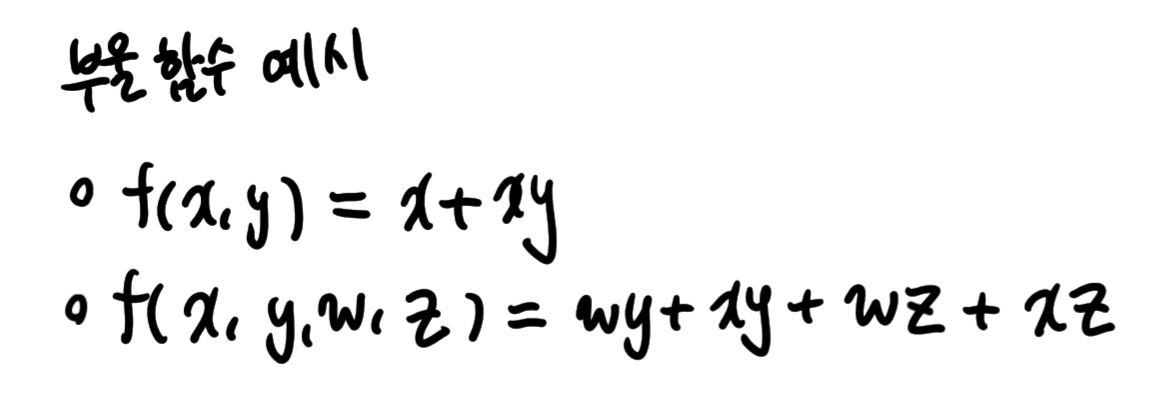
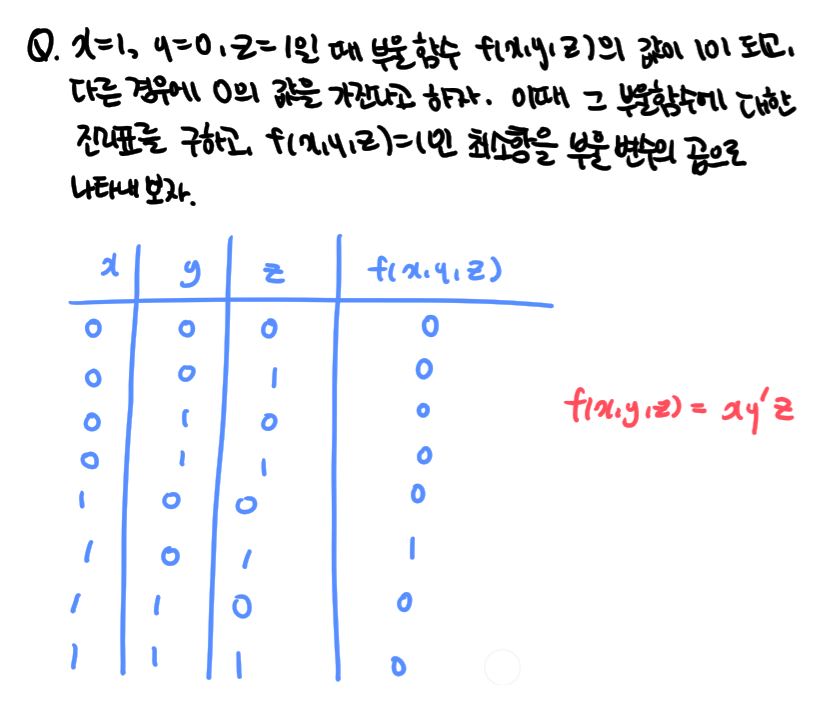
2) 곱의 합(sum of products) 또는 논리합 표준형(Disjunctive Normal Form : DNF)
- 부울 함수를 나타내는 데 있어서 최소항들의 합으로 표현하는 것이다.
- 최소항들은 부울 변수의 곱으로 표현되고, 부울 함수는 부울 변수들의 곱의 합으로 표현된다.
11.3 부울 함수의 간소화
- 부울 변수의최소항들로부터 얻어진 부울 함수는 좀 더 간단한 형태의 식으로 만들 수 있다.
- 간소한 형태의 식이란 같은 기능이나 결과를 도출하면서도 더 적은 변수와 연산자를 사용한 식을 말한다.
1) 부울 함수식을 간소하게 표현하는 방법
(1) 부울식의 기본 법칙 사용 : 과정이 복잡하고 간소화에 대한 확인이 쉽지 않다.
(2) 카노우맵(Karnaugh map)을 사용
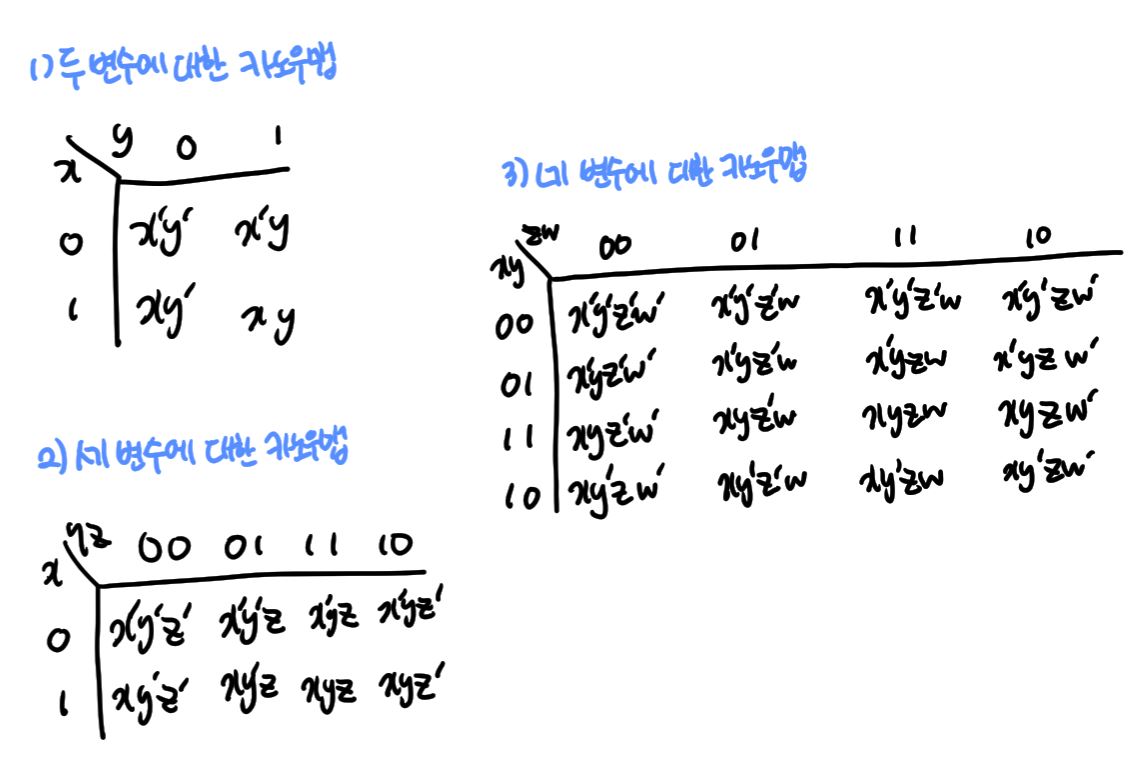
2) 카노우맵(Karnaugh map)
- 1953년 카노우(Maurcie Karnaugh)에 의해 제안되었는데, 사각형 모양의 표를 이용하여 부울 함수를 비교적 쉽게 간소화할 수 있는 방법이다.
- 통상 6개 이하의 변수를 다루는 데에만 사용할 수 있다.
- 카노우맵을 그릴 때는 부울 변수들로부터 나타나는 모든 경우의 최소항들을 사각형으로 연결시켜서, 최소항들 중 1의 값을 가지는 사각형 안에 '1'을 표시한다.
- '1'로 표시된 사각형들에서 부울식의 공통점을 찾아내어 부울함수를 간소화하는데, 사각형을 연결시킬 때는 인접한 사각형끼리는 한 변수의 변화만 있게 만들어야 한다.
- 카노우맵을 사용하여 인접한 항들끼리 묶을 때는 항상 2의 배수로 묶는다.
11.4 논리 회로 설계
1) 논리 회로 설계
- 논리 회로(logic circuit)란 부울 대수의 기본 연산인 논리합, 논리곱, 논리부정 등의 연산을 실행하기 위한 회로로서 논리 게이트(logic gate)라고도 한다.
- 논리 회로는 2진 정보를 취급하며 통상 2개 이상의 입력 단자와 하나의 출력 단자로 구성된다.
- 부울 함수로 표현된 식은 컴퓨터에서 사용되는 기본적인 논리회로를 설계하는 데 활용한다.
- 컴퓨터 회로를 설계하는 데 있어서의 입력과 출력은 논리 회로의 게이트(gate)들을 상호 연결함으로써 구성할 수 있다.- 입력은 부울 변수로, 출력은 부울 함수로, 부울 연산자는 게이트로 표현한다.- 논리값이 1일 때는 회로의 스위치가 연결된(on) 상태이고, 0일 때는 연결되지 않은(off) 상태를 나타낸다.
- 모든 부울 함수는 최소항의 부울 합으로 나타낼 수 있으며, 각 최소항은 부울 곱으로 만들 수 있다.
- 논리 함수의 완전성(completeness) : 부울 연산자 AND, OR, NOT만으로도 사실상 모든 논리 함수들을 나타낼 수 있다.
2) 논리 회로
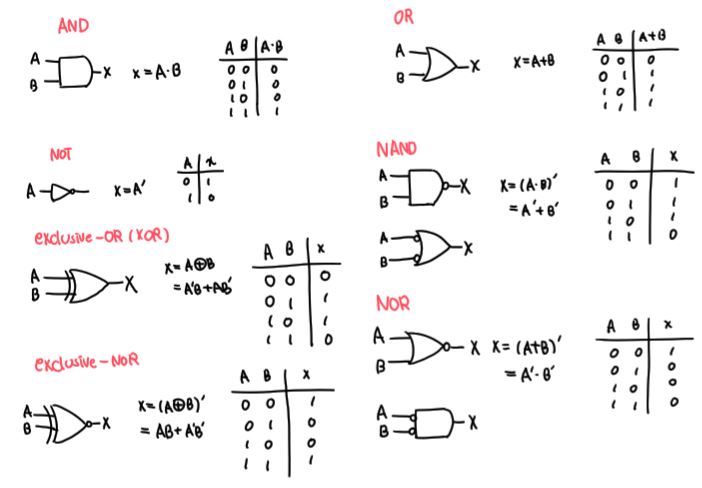
(1) 논리곱 회로 (AND gate)
- 논리곱 회로는 논리곱(AND) 조건을 만족시키는 회로로서 2개의 입력 A, B가 모두 1인 경우에만 출력 Y가 1이 된다.
- 논리곱 연산자는 '·' 으로 표현한다.
- AND 게이트는 스위치가 직렬로 연결되어 있으므로 두 스위치가 모두 1(ON)이 되어야 회로가 연결된다.
(2) 논리합 회로 (OR gate)
- 논리합 회로는 논리합(OR) 조건을 만족시키는 회로로서 입력 A와 B 중 적어도 하나가 1인 경우에 출력 Y가 1이 되는 논리 회로이다.
- 논리합 연산자는 '+'로 표현한다.
- OR 게이트는 스위치가 병렬로 연결되어 있으므로 두 스위치 중 하나만 1이 되면 회로가 연결된다.
(3) 논리부정 회로 (NOT gate)
- 논리부정 회로는 논리부정(NOT) 조건을 만족시키는 회로로서 입력 A가 1일 경우에 출력 Y가 0이 된다.
- 입력 A가 0일 경우에는 출력 Y가 1이 된다.
- 논리부정 연산자는 ' ' ' 또는 ' - '로 표현한다.
(4) 이외의 회로
- XOR 게이트
- '(Exclusive) OR' 게이트
- 두 부울변수가 서로 다른 값을 가질 경우에만 출력이 1이 된다.
- OR 게이트의 왼쪽에 활 모양의 곡선을 추가한 것이다.
- NAND 게이트 : AND 게이트의 부정
- NOR 게이트 : OR 게이트의 부정
- Exclusive-NOR 게이트 : exclusive-OR 게이트의 부정
11.5 논리 회로의 응용
1) 논리회로의 응용
- 논리 회로의 응용 범위는 매우 넓은데, 어느 제품이든지 회로에 들어가는 것은 모두 논리 회로를 응용한 것이다.
- 일상생활에서 사용하는 TV를 비롯한 가전 제품들이 대부분 논리 회로를 응용한 것이다.
2) 전자투표
- 3명으로 구성된 어떤 위원회에서 의사 결정을 할 때, '찬성' 또는 '반대' 중의 하나로 투표를 하는데 2명 이상이 '찬성'을 할 경우 안건이 통과된다고 가정한다.
- 안건이 통과되는지의 여부를 즉석에서 결정할 수 있는 소규모 전자투표기의 논리 회로는 아래 그림으로 표현된다.
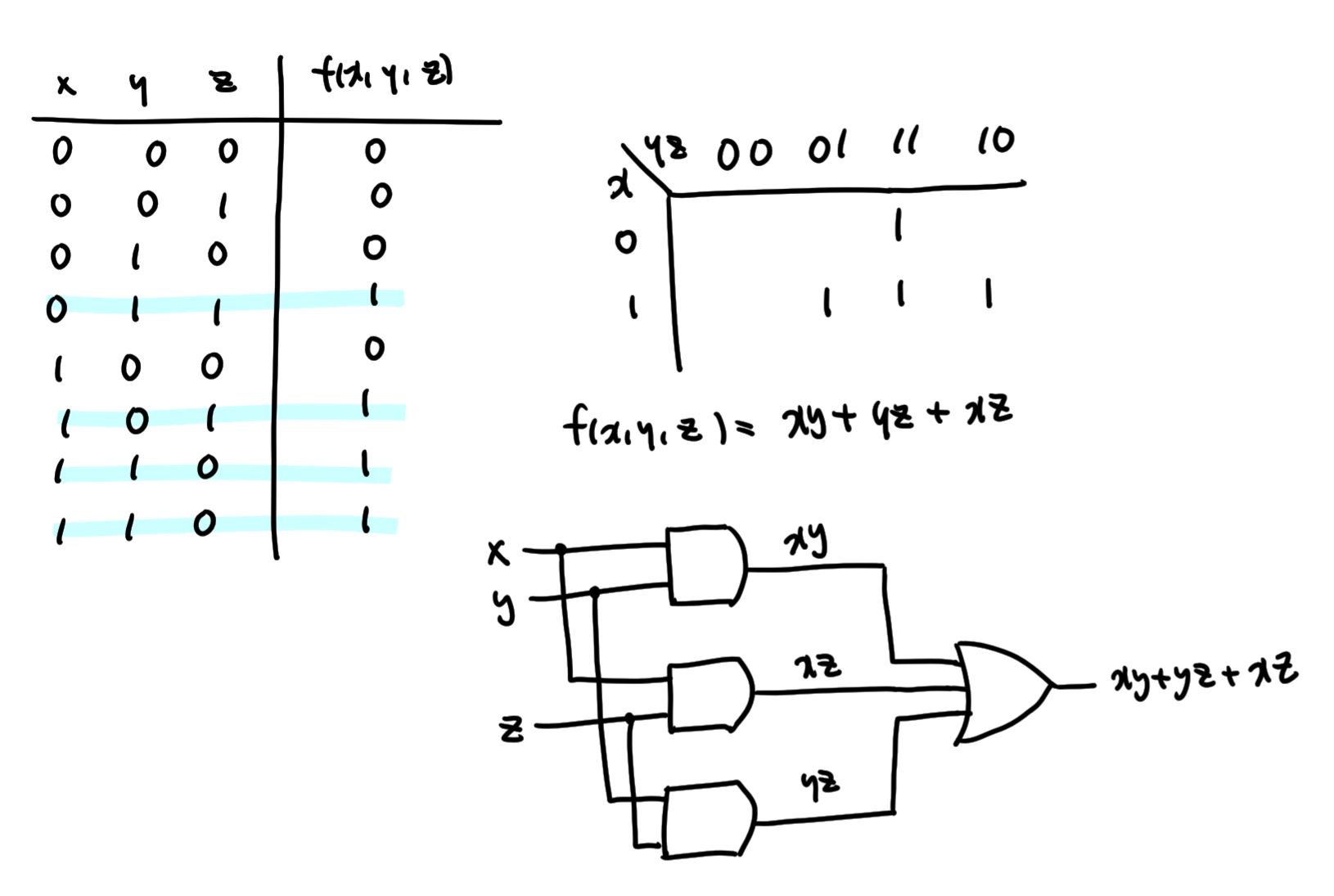
- 전자 투표 회로에서 x, y, z 중 2개씩 묶어서 AND 회로들로 구성된다.
- 3개의 AND 게이트 중 어느 2개만 1이 되기만 하면다음 단계인 OR 게이트에서는 1이 나온다.
3) 가산기(Adder)
- 컴퓨터의 중앙처리장치(CPU)에 있는 산술논리장치(Arithmetic Logic Unit ; ALU) 내에는 숫자들을 더하는 기능을 가진 가산기가 내장되어 있다.
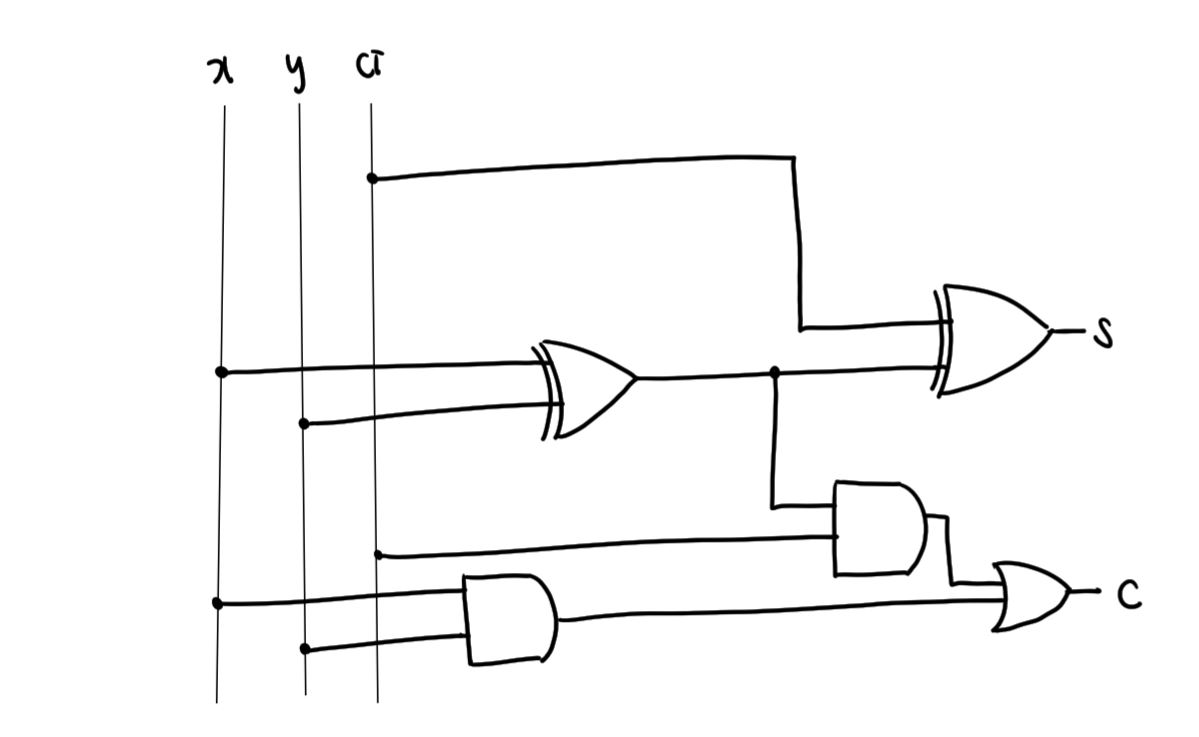
11.6 부울 대수의 응용과 4차 산업혁명과의 관계
1) 복잡하고 빠른 논리회로를 이용하는 슈퍼컴퓨터
- 부울 대수를 이용하여 복잡한 논리 회로를 이용하는 예로는 슈퍼컴퓨터(Super computer)를 들 수 있다.
- 슈퍼컴퓨터란 그 당시의 가장 우수한 범용 컴퓨터보다 한두 단계 앞선 최첨단 컴퓨터를 말한다.
2) 디지털 가전제품에 논리 회로가 필수적이다.
- 부울 대수를 이용한 논리 회로의 응용은 우리의 일상생활에서 이루 셀 수 없을만큼 많다.
- 전기와 회로를 이용하는 대부분의 제품은 부울 대수를 이용한 논리회로를 사용한다.
3) 부울 대수와 4차 산업혁명과의 관계 : 신경망 기술
- 신경망(Neural Network)은 컴퓨터를 사용하여 인간의 신경세포인 뉴런(neuron)을 모델링하는 4차 산업혁명의 핵심 기술 분야 중 하나다.
- 인간의 지능으로 할 수 있는 영역 중 학습이나 인식 등을 컴퓨터가 할 수 있도록 하는 방법을 연구하는 분야이다.
- 신경망을 구현하기 위해서는 부울 대수를 활용하는 초고속의 논리 회로가 필요하다.
'전공과목 정리 > 이산수학' 카테고리의 다른 글
| [이산수학🔗] 오토마타, 형식 언어, 문법 (13장) (2) | 2023.01.19 |
|---|---|
| [이산수학🔗] 알고리즘을 통한 문제 해결 (12장) (0) | 2023.01.19 |
| [이산수학🔗] 행렬과 행렬식 (10장) (2) | 2023.01.15 |
| [이산수학🔗] 순열, 이산적 확률, 재귀적 관계 (9장) (0) | 2023.01.13 |
| [이산수학🔗] 트리 (8장) (2) | 2023.01.13 |