포스팅에 참고하는 교재 : 4차 산업혁명 시대의 이산수학 개정판 (생능출판)
12.1 알고리즘이란 무엇인가?
1) 알고리즘
- 주어진 문제를 해결하기 위해 필요한 여러 가지 단계들을 체계적으로 명시해 놓은 것
- 사전적 의미는 '어떤 문제를 해결하는 한 방법의 상세한 특징을 기술하는 것'이다.
2) 알고리즘이 가져야 할 7가지 주요 특성
- 입력 (input) : 문제를 풀기 위한 입력이 있어야 한다.
- 출력 (output) : 문제를 해결했을 때 답이 나와야 한다.
- 유한성 (finiteness) : 유한 번의 명령이 수행된 후에는 끝나야 한다.
- 정확성 (correctness) : 주어진 문제를 정확하게 해결해야 한다.
- 확정성 (definiteness) : 각 단계가 실행된 후에는 결과가 확정된다.
- 일반성 (generality) : 같은 유형의 문제에 모두 적용된다.
- 효율성 (effectiveness) : 정확하면서도 효율적이어야 한다.
12.2 알고리즘의 표현
1) 알고리즘의 표현
- 순서도 (flow chart), 유사 코드(pseudo code), 언어 (language) 등 여러 가지 방법으로 표현될 수 있다.
- 누구나 이해할 수 있도록 명확하게 기술하는 것이 매우 중요하다.
- 어떤 문제가 주어졌을 때 그 문제를 풀기 위한 방법론인 알고리즘이 항상 하나만 있는 것은 아니다.
- 컴퓨터 프로그램의 경우에는 어떤 알고리즘이 가장 효율적인지를 선택되어야 한다.
- 일반적으로 수행 시간, 메모리 용량, 자료의 종류, 프로그래머의 성향에 따라 가장 알맞은 알고리즘을 선택한다.
2) 유사 코드(pseudo code)
- 알고리즘을 프로그래밍 언어와 유사한 형태로 풀어 써 놓은 것으로서, 정형화된 문법적 측면을 배제하고 사고의 흐름을 간결하고 효과적으로 전달하는 표현이다.
- 유사 코드를 나타내는 추가적인 표현은 다음과 같다.
- 유사 코드는 알고리즘을 개략적으로 표현하는 데에 쓰인다.
- 유사 코드로 적는 것은 알고리즘의 각 단계를 차례로 적는 것이다.
- 유사 코드는 일반적으로 C언어나 자연어와 유사하게 기술할 수 있다.
3) 순서도(flow chart)
- 처리하고자 하는 문제를 분석한 후 처리 순서를 단계화하고, 상호간의 관계를 표준 기호를 사용하여 입력, 처리, 결정, 출력 등의 박스와 연결선으로 일목요연하게 나타낸 도표(diagram)
-순서도는 처리 순서를 논리적으로 표현하는 도표로서 작업의 흐름을 나타내기 때문에 '흐름도'라고도 불리고 있다.
- 순서도는 주로 컴퓨터 프로그램을 위해 많이 쓰이지만, 반드시 컴퓨터의 이용을 전제로 하는 것은 아니다.
12.3 알고리즘 분석
- 알고리즘에 대한 평가와 비교는 컴퓨터 프로그램을 통한 문제 해결에 있어서 매우 중요한 관심 분야이다.
- 어떤 문제를 해결하는 데 있어서 두 가지 질문을 통해 알고리즘을 분석할 수 있다.
- 어떤 문제의 해결에 있어서 주어진 알고리즘을 사용하는 데 드는 비용이 얼마인가?
- 그 문제를 해결하는 데 비용이 가장 적게 드는 알고리즘은 무엇인가?
- 비용 : 연산하는 데 드는 필요한 시간과 기억장소의 크기
- 주어진 문제를 해결하는 방법에는 여러 가지 알고리즘이 있으나 그 중에서 비용이 적게 드는 알고리즘을 찾기 위해서는 효율성 분석(performance analysis)이 필요하다.
- 효율성을 분석하기 위해서는 알고리즘 수행 시 필요한 시간 복잡성(time complexity)과 공간 복잡성(space complexity)의 두 가지 요소를 검토한다.
- 수행 시간과 그에 따르는 기억 장소의 크기는 알고리즘이 처리하는 입출력 자료의 크기에 따라 달라짐.
- 일반적으로 알고리즘을 분석할 때 입력의 개수를 n으로 분석할 때 효율성을 그에 대한 함수로 나타냄.
- 최근에는 컴퓨터 하드웨어의 발달로 알고리즘 분석에서 어떤 문제를 해결하는 데 필요한 기억장소의 크기에는 그리 큰 비중으로 두고 있지 않다.
12.4 알고리즘의 복잡성
알고리즘의 복잡성
- 알고리즘의 복잡성을 측정하는 데 있어서 일반적으로 빅오(Big-Oh) 표현을 상요하며, 대문자 O를 써서 표시한다.
- f(n)=O(n) : f(n)의 차수(order)가 n이고, 'Big-Oh of n'이라 읽는다.
- 음수값을 가지지 않는 함수 f와 g에서 모든 n에 대해서 n>n0이고, f(n) < c·g(n)이 되는 양의 상수 c와 n0가 존재한다면, f(n)=O(g(n))이다.
- O(g(n))은 충분히 큰 수 n이 주어질 때 g(n)에 양의 상수 배를 한 함수들 중에서 가장 작은 함수를 의미한다.
- O(1) < O(log2n) < O(n) < O(nlog2n) < O(n2) < ... < O(2n) < O(n!)
- O(1) : 문제를 해결하는 데 걸리는 수행 시간이 입력 자료의 수 n의 크기에 관계없이 상수이다.
- 오른쪽으로 갈수록 n이 커짐에 따라 수행시간이 급격히 증가한다.
- 보다 효율적인 알고리즘은 다른 알고리즘보다 수행 시간이 적게 필요한 알고리즘이다.
12.5 재귀 함수의 복잡성
재귀함수 (Recursive function)
- 주어진 문제를 해결하는 데 있어서 f(n)이 필요한 함수라고 했을 때, f(n)의 식에 f(n-1), f(n-2), ... , f(1) 중 한 개 이상의 내용이 포함되는 함수이다.
- 재귀함수에서 현재 함수의 값은 항상 그전에 있던 함수에 의해 영향받는다.
12.6 탐색 알고리즘
1) 탐색 (search)
- 주어진 파일 또는 원소들 중에서 어떤 특정한 원소를 찾는 것.
- 탐색의 두 가지 방법
- 순차 탐색 (sequential search) : 원소들이 정렬되어 있지 않을 경우에 원소들을 처음부터 비교하여 찾는 것
- 이진 탐색 (binary search) : 원소들이 정렬되어 있을 경우에 찾는 방법으로서 순차탐색보다 탐색 자체가 빠르다.
2) O(n) 알고리즘
- 순차 탐색은 배열에 있는 특정한 원소를 찾기 위해서 배열의 처음 원소부터 차례로 모든 원소들을 비교하여 탐색한다.
- 효율적이지는 않지만 효과적으로, 모든 원소를 조사하는 탐색을 선형 탐색(linear seach)이라고 한다.
int seq_search(int array[], int search_num, int n)
{
int i;
array[n] = search_num;
for (i=0; array[i] != search_num; i++);
return ((i<n)?i:-1);
}- 프로그램에서 for 문을 제외한 다른 문장은 한 번만 수행된다.
- for 문에서의 비교횟수를 조사함으로써 전체 수행 횟수를 알 수 있다.
- array[i]=search_num일 때 필요한 비교 횟수는 i+1이다.
- 평균 비교횟수
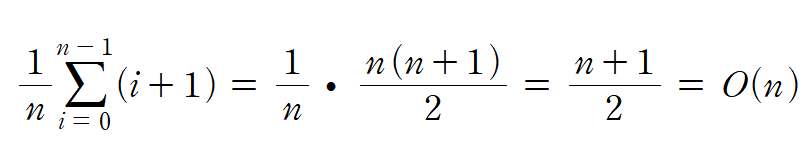
3) O(log2n) 알고리즘
- 원소들이 순서대로 정렬되어 있을 때는 처음부터 값을 찾을 필요가 없이 중간의 원소와 비교하여 그보다 작을 때에는 그 원소의 왼쪽 원소들 중에서, 클 때는 오른쪽 원소 중에서 다시 같은 형식으로 찾으면 훨씬 시간을 절약하여 찾을 수 있다.
- O(log2n)인 이진탐색은 O(n)인 순차탐색보다 빠르고 효율적이다.
- 이진 탐색 (binary search) : 배열 가운데의 원소 값과 찾으려는 값을 비교하여, 비교된 결과에 따라 왼쪽 원소의 배열 또는 오른쪽 원소의 배열 중에서 다시 찾기를 계속한다.
int binary_search(int array[], int search_num, int left, int right)
{
int middle;
while (left <= right)
{
middle = (left+right)/2;
if (array[middle] < search_num) left = middle+1;
else if (array[middle] > search_num) right = middle-1;
else return middle;
}
return -1;
}- 분할 정복 알고리즘(Divideand conquer algorithm) : 전체 집합을 찾으려는 원소와 비교하여 부분 집합으로 나눠 찾는 알고리즘이다.
- 분할 정복 알고리즘은 다시 나누어진 부분 집합에서 같은 방법을 적용한다.
- 이진 탐색 알고리즘의 수행 시간은 while반복문이 1회 수행될 때마다 탐색해야 할 배열의 크기가 반으로 줄어든다.
- 탐색해야 할 배열의 크기가 1일 때 알고리즘이 수행을 끝낸다.
- 평균 비교 횟수

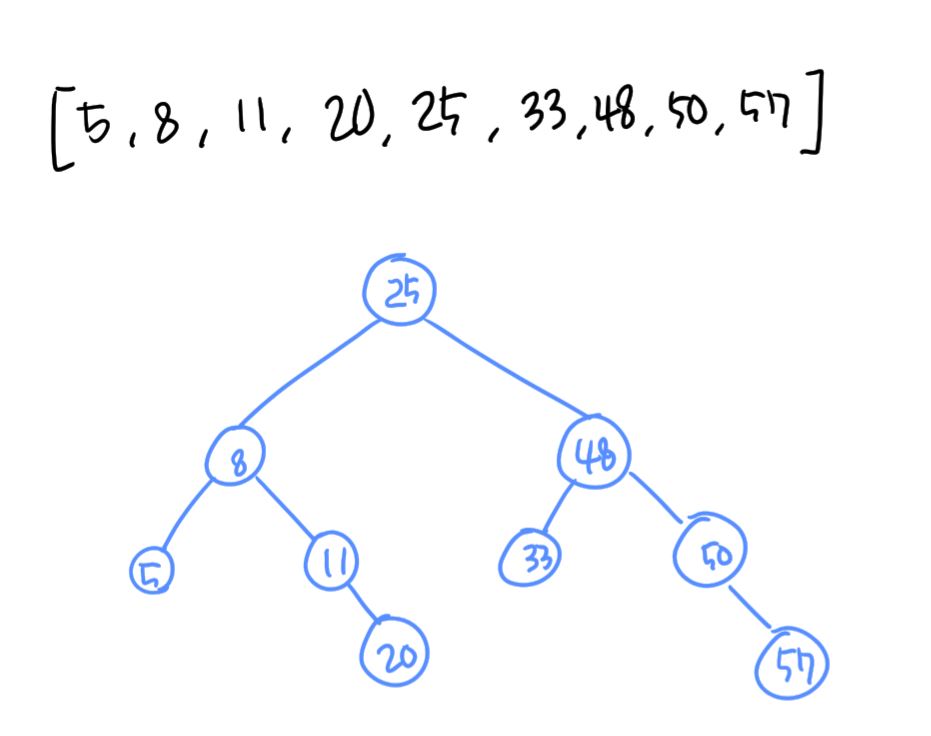
- 이진 탐색 알고리즘을 이용하여 원소를 찾는 과정은 이진 탐색 트리(binary search tree)를 이용하면 간단히 표현할 수 있다.
- 이진 탐색 트리는 처음 배열의 중간 원소를 루트(root)로 놓는다.
- 각 서브 트리의 루트는 둘로 나우더진 부분 집합들의 중간 원소들로 이루어진다.
- 이진 탐색 트리의 루트로부터 트리의 노드로 가는 경로는 이진 탐색 알고리즘의 비교 횟수와 동일하므로 최악의 경우 트리의 깊이(depth)에 해당하는 비교 횟수인 O(log2n)이 된다.
12.7 정렬 알고리즘
1) 정렬 (sort)
- 임의로 나열되어 있는 데이터들을 주어진 항목에 따라 크기 순서대로 작은 순서부터(오름차순, ascending order) 또는 큰 순서부터(내림차순, descending order) 늘어놓는 것이다.
- 정렬되어 있는 데이터들은 다음과 같은 작업을 수행할 때 응용된다.
- 데이터의 탐색
- 리스트(list)에 있는 다른 항목들을 비교
2) O(n2) 알고리즘 : 버블 정렬(bubble sort), 삽입 정렬(insertion sort)
(1) 버블 정렬
- 이웃한 두 개의 원소를 비교하여 순서가 서로 다르면 원소의 자리를 서로 바꾸고, 그렇지 않으면 그 위치에 그대로 놓는다.
void bubble_sort(int array[], int n)
{
int i, j, temp;
for (i=0; i<n-1; i++)
{
for (j=0; j<n-1-i; j++)
{
if (array[j]>array[j+1])
{
temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
}
}
}- 위의 알고리즘에서 i가 한 번 수행될 때마다 제일 오른쪽 끝에서부터 원소 중 큰 순서대로 정렬이 된다.
- 수행시간 (i=0일 때 j에 대한 반복문은 n-1번, i=1일 때 n-2번 수행된다.)

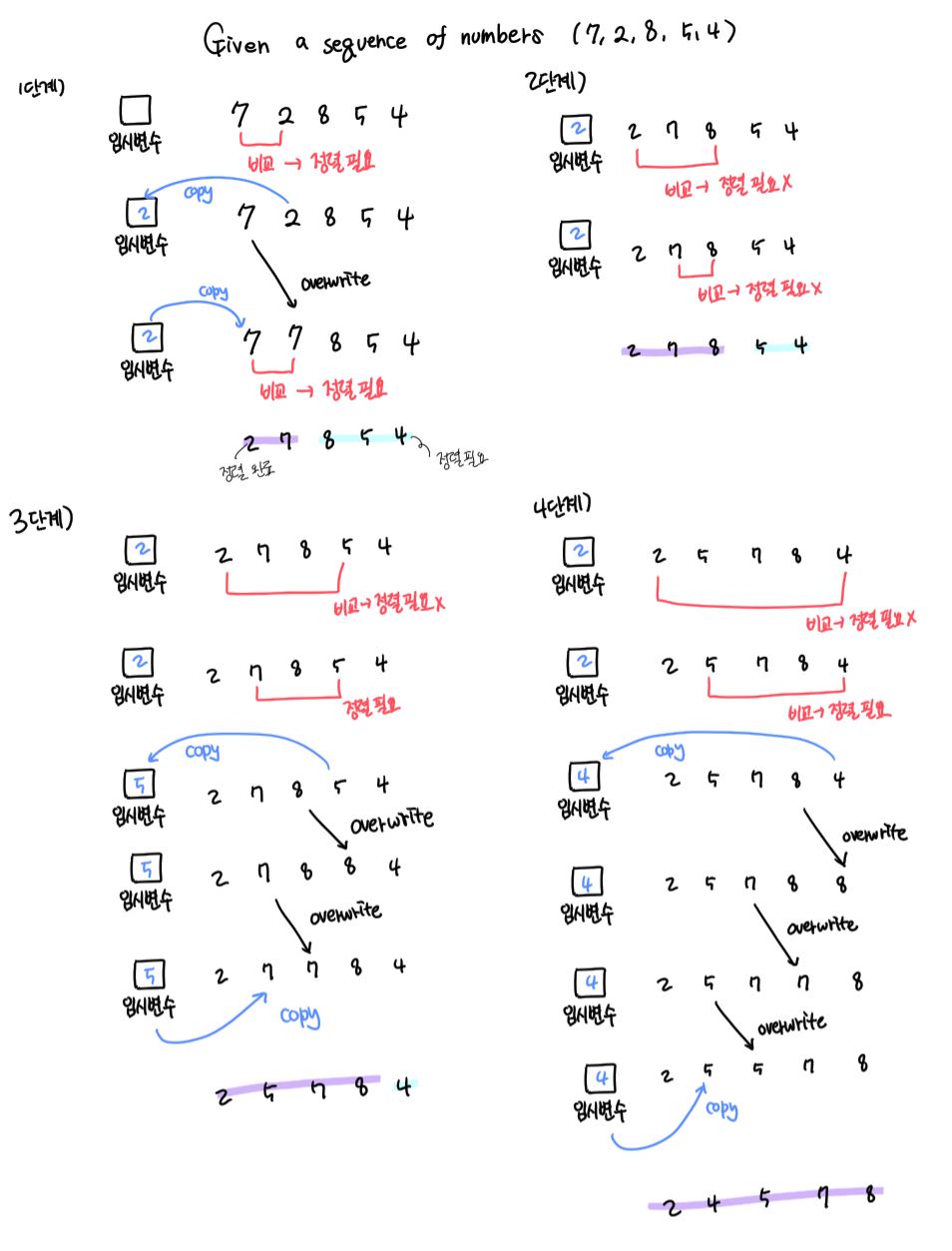
(2) 삽입 정렬

3) O(nlog2n) 알고리즘 : 퀵 정렬(quick sort), 병합 정렬(merge sort), 힙 정렬(heap sort)
1) 퀵 정렬
- 모든 정렬 방법 중에서 평균 수행 시간이 가장 빠른 방법이다.
- 현재 정렬 과정에서 처리되고 있는 피벗 키(pivot key) p를 기준으로 원소를 두 부분으로 나눈다.
- 나누어진 두 부분(subfile)을 따로 다시 퀵 정렬로 재귀함으로써 모든 원소가 순서대로 정렬될 때까지 실행한다.
- 퀵 정렬의 평균 수행 시간은 O(nlog2n)이나 정렬해야 할 원소들의 값에 따라 최악의 경우에는 O(n2)이 된다.
- 알고리즘 개요
- 주어진 배열에서 pivot(특정한 원소)을 하나 잡는다. pivot은 일반적으로 가장 가장자리 원소나, 중앙의 원소를 잡아주며 랜덤으로 선택하기도 한다.
- 주어진 배열의 원소들을 pivot과 비교하여 작은 값들은 pivot의 왼쪽, 큰 값들은 pivot의 오른쪽으로 오도록 재배열한다.
- pivot의 왼쪽과 오른쪽의 서브배열에 대해서 동일한 배열을 재귀적으로 적용한다.
- 예시
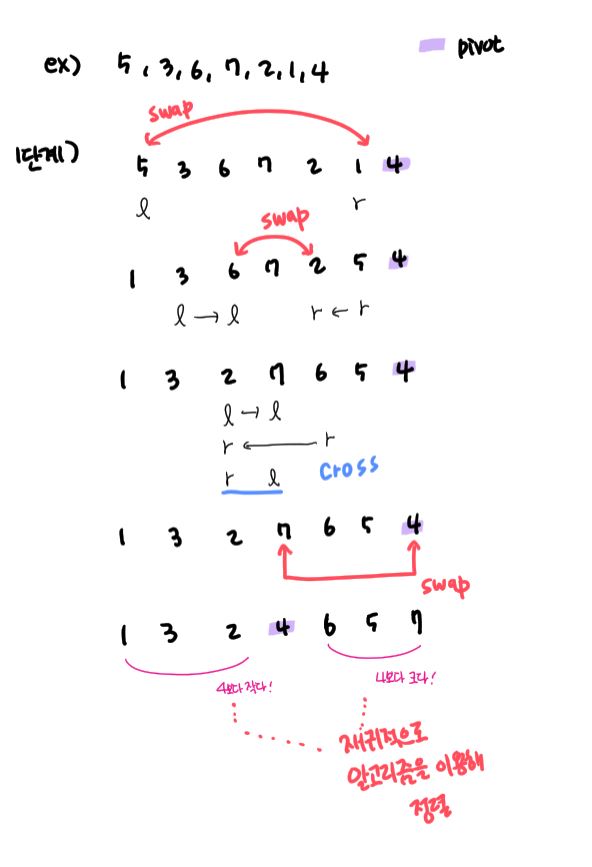
- 가장 오른쪽 원소를 pivot으로 설정한다.
- pivot을 제외한 나머지 원소로 구성된 sub-array에서 가장 좌측의 원소를 l, 가장 우측의 원소를 r로 지정한다.
- l이 pivot보다 클 때까지 오른쪽으로 한 칸씩 이동시킨다.
- r이 pivot보다 작을 때까지 왼쪽으로 한 칸씩 이동시킨다.
- l과 r이 교차(l이 r보다 우측에 위치)하지 않았다면 l의 원소와 r의 원소를 바꾼다.
- l과 r이 교차했다면 l과 pivot을 바꾼다.
2) 병합 정렬
- 크기가 1인 정렬된 두 파일을 병합하여 크기가 2인 파일들을 생성한다.
- 이 파일들에 대하여 병합 과정을 반복 시행하여 한 개의 파일들을 만들어내는 방법이다.
- 병합(merging)이란 여러 개의 정렬되어 있는 배열 자료들을 혼합하여 하나의 정렬된 배열로 합하는 작업을 의미한다.
- 두 개의 서로 다른 정렬된 배열을 합하여 하나의 정렬된 배열로 만드는 병합 방식을 2-way 병합과정이라 한다.
-n-way 병합 : n개의 서로 다른 배열을 하나의 정렬된 배열로 합치는 병합 방식
-평균 수행 시간은 O(nlog2n)이다.
- 알고리즘 개요
- 주어진 배열을 두 개의 서브배열로 나눈다.
- 각각의 서브배열을 재귀적으로 정렬한다.
- 정렬된 서브배열을 merge한다.
- 예시

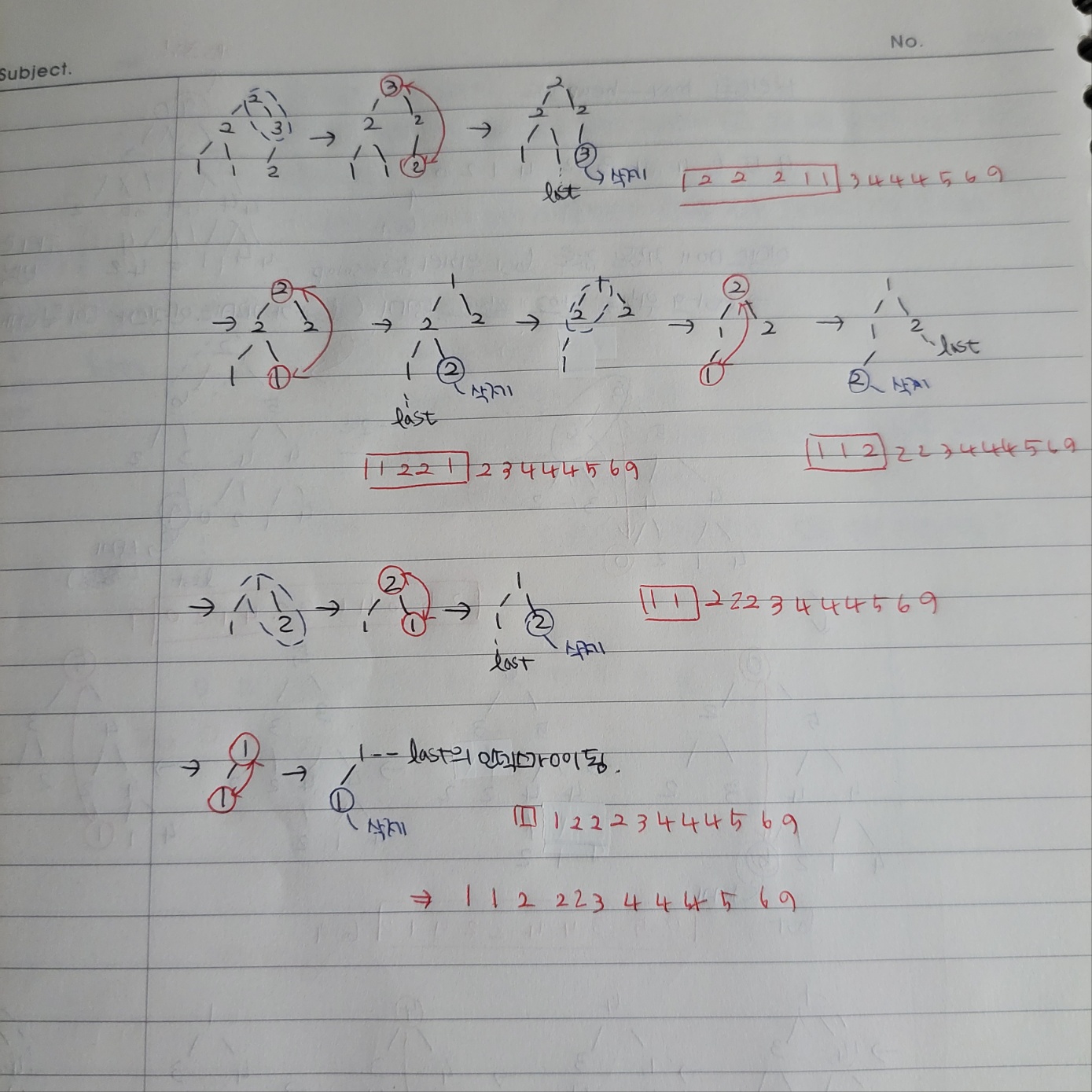
3) 힙 정렬
- 자료를 정리할 때 모든 자료들을 동시에 처리하지 않고 모든 자료 중에서 가장 큰 자료를 찾아 출력한다.
- 나머지 자료 중에서 앞의 과정을 반복하여 가장 큰 자료를 찾아 출력시키며 정렬하는 방식이다.
-평균 수행 시간은 O(nlog2n)이다.
- binary tree를 이용한다. -> max heap
- binary tree는 root, left child, right child의 3개의 노드 타입으로 나뉜다.
- max heap은 root가 자신의 자식 노드들보다 큰 값을 갖는 binary tree이다.
- 예시


12.8 알고리즘의 응용과 4차 산업혁명과의 관계
1) 문제 해결의 효율적인 방법론
- 알고리즘이란 주어진 문제를 해결하기 위해 필요한 여러 가지 단계들을 체계적으로 명시해놓은 것을 말하는데, 일상생활에서 만나는 수많은 문제들의 효과적인 해결 방안들을 포함한다.
2) 컴퓨터와 공학 분야에의 응용
- 알고리즘은 컴퓨터를 통한 프로그램의 핵심 단계에서 매우 중요한 역할을 담당한다.
- 컴퓨터는 문제를 풀기 위해 알고리즘을 사용한다.
3) 알고리즘과 4차 산업혁명과의 관계 : 로보틱스
- 로보틱스(robotics) : 인공지능적인 능력을 가진 로봇 기술과 관련된 4차 산업혁명의 한 분야
- 지능형 로봇(Intelligent robotics)은 스스로 판단하고 행동하며, 외부 환경에 적응할 수 있는 로봇으로서 다양한 환경 분야에서 여러 가지 업무를 수행할 수 있다.
- 로보틱스 분야에서는 알고리즘의 중요성이 매우 크며, 모든 판단과 행동에 있어 효율적인 알고리즘의 적용이 필요하다.
* 알고리즘 관련 포스팅
https://0yeonjae2.tistory.com/entry/IT%EA%B0%9C%EB%A1%A0-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
[IT개론] 알고리즘
출처 : 소프트웨어 세상을 여는 컴퓨터과학 1. 알고리즘의 개요 1) 알고리즘의 개념 (1) 알고리즘(algorithm) - 어떤 문제를 해결하기 위해 구성된 일련의 절차 (2) 알고리즘의 조건 - 0개 이상의 입력,
0yeonjae2.tistory.com
'전공과목 정리 > 이산수학' 카테고리의 다른 글
| [이산수학🔗] 오토마타, 형식 언어, 문법 (13장) (2) | 2023.01.19 |
|---|---|
| [이산수학🔗] 부울 대수 (11장) (1) | 2023.01.18 |
| [이산수학🔗] 행렬과 행렬식 (10장) (2) | 2023.01.15 |
| [이산수학🔗] 순열, 이산적 확률, 재귀적 관계 (9장) (0) | 2023.01.13 |
| [이산수학🔗] 트리 (8장) (2) | 2023.01.13 |