포스팅에 참고하는 교재 : 4차 산업혁명 시대의 이산수학 개정판 (생능출판)
13.0 개요
- 오토마타, 형식언어, 문법에 관한 연구는 매우 추상적인 특성을 가지고 있으며 디지털 모델링, 컴파일러, 문서 편집기, 엘리베이터 등 다양한 분야에서 응용되고 있다.
- 이론적인 계산 모델인 오토마타 중에서 유한 오토마타는 컴파일러의 어휘분석을 수행하는 데 있어서 결정적인 역할을 하였다.
- 오토마타, 형식 언어, 문법은 상호 밀접한 관계에 있는데, 각종 컴퓨터 프로그램 언어들이 정해진 문법에 따른 형식 언어에 기반을 두고 만들어졌기 때문이다.
- 튜링머신은 현재의 디지털 컴퓨터의 역량과 대등한 계산 모델이다.
13.1 오토마타란 무엇인가?
1) 오토마타 (automata)
- 디지털 컴퓨터의 수학적 모델인 오토마톤(automaton)의 복수형으로서 '자동기계 장치'란 뜻을 가진다.
- 일반적으로 입력 장치, 출력 장치, 저장 장치, 제어 장치를 가지고 있으므로 현대적인 디지털 컴퓨터가 작동하는 이론적인 매커니즘이라 볼 수 있다.
- 단순한 형태의 오토마타는 기원전 3천 년 무렵부터 만들어졌는데, 고대 이집트인이 사용했던 모래시계나 물시계 등도 넓은 의미의 오토마타에 속한다.
- 오토마타는 수학적 방법론에 바탕을 둔 디지털 컴퓨터의 추상적인(abstract) 모델이다.
2) 오토마타의 특성
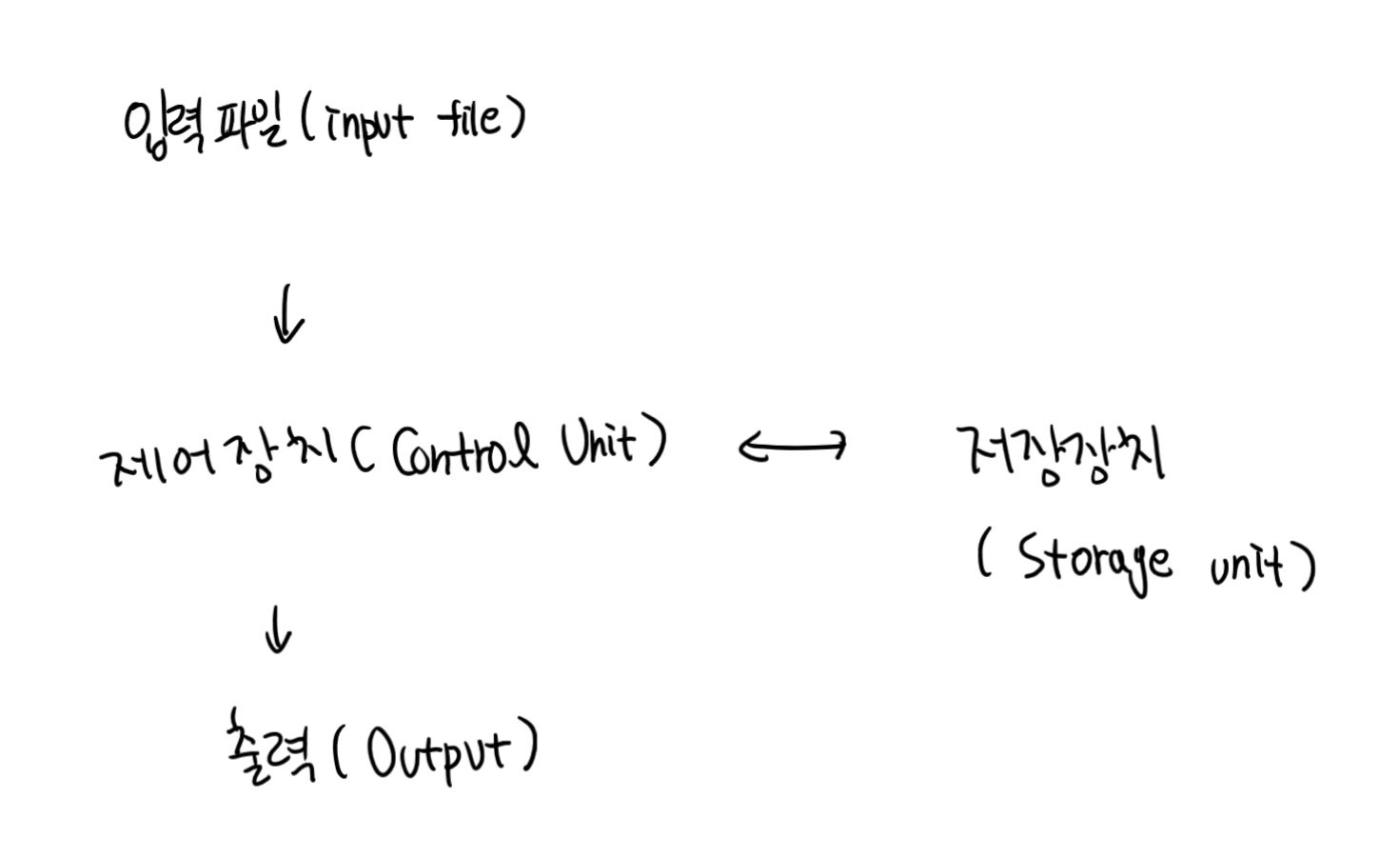
- 오토마타는 입력 데이터를 읽을 수 있는 기능을 가지고 있다. 입력 데이터는 입력 파일에 쓰인 알파벳상의 스트링들로 이루어져 있는데, 입력 파일은 네모꼴의 셀(cell)들로 이루어져 있으며 각 셀에는 오직 하나의 심볼만 존재한다.
- 오토마타는 특정 형태의 출력 기능을 가지고 있다. 0이나 1의 출력을 생성할 수 있으며 인식(accept) 또는 기각(reject)의 출력도 생성한다.
- 오토마타는 무한 개의 셀들로 이루어진 임시 저장 장치를 가질 수 있다. 각 셀은 하나의 심볼만을 가질 수 있는데, 오토마타는 작동에 따라 셀들의 내용을 읽어내거나 변경할 수 있다.
- 오토마타는 유한개의 내부 상태를 제어할 수 있는 제어 장치를 가지고 있다. 이것은 제어에 따라 상태가 변화될 수 있다.
- 오토마타는 이산적인(discrete) 시간 단위로 작동됨을 기본 가정으로 한다.
- 어느 특정 시각에 제어 장치는 특정의 상태에 놓여 있으며, 입력 기능은 입력 파일상의 어떤 특정한 심볼을 읽는다.
3) 전이 함수(transition function)
- 제어 장치의 다음 상태는 전이 함수에 의해 결정된다.
- 전이 함수는 현재의 제어 상태, 입력 심볼, 임시 저장 장치 내의 정보들에 의해 결정된다.
- 결정적 오토마타(deterministic automata)
- 전이에 의한 다음 상태가 현재의 형상에 따라 유일하게 결정되는 오토마타이다.
- 현재의 내부 상태, 입력 심볼, 임시 기억 장치에 관한 정보를 알면 오토마타의 다음 행동을 정확히 예측할 수 있다.
- 비결정적 오토마타(nondeterministic automata)
- 현재의 형상에서 2가지 이상의 이동도 가능한 오토마타이다.
- 우리는 가능한 이동의 집합을 예측할 수 있을 뿐이다.
4) 인식기(accepter)와 트랜스듀서(transducer)
- 오토마타는 출력 여부에 따라 인식기와 트랜스듀서로 나누어진다.
- 인식기는 주어진 입력에 대해 인식하거나 기각할 수 있는 기능만을 가지지만, 트랜스듀서는 밀리 기계와 같이 인식이나 기각의 기능 외에 출력도 할 수 있는 오토마타 모델이다.
13.2 오토마타 학습의 필요성과 유한 상태 시스템
1) 오토마타 학습의 필요성
- 오토마타 이론이 전산학이나 전자공학 등의 학문을 이해하는 데 있어서 필요한 기본적인 개념과 원리를 제공하기 때문이며, 또한 이를 여러 가지 응용 분야에 적용할 수 있기 때문이다.
- 오토마타 이론을 통하여 컴퓨터와 관련된 이론적인 바탕과 작도으이 원리를 보다 정확하게 이해함으로써 하드웨어나 소프트웨어 각 분야에 대한 직관을 넓힐 수 있으며, 보다 포괄적인 통찰력을 제공해준다.
- 오토마타 이론의 직접적인 응용이다.이를 통하여 디지털 컴퓨터의 디자인, 프로그래밍 언어, 컴파일러, 신경생리학, 통신,신경망, 언어론 등 다양한 분야에 직접 활용할 수 있다.특히 컴파일러나 프로그래밍 언어를 정확하게 이해하기 위해서는 오토마타 이론의 이해가 필수적이다.
- 추상적 모델의 개념적 이해이다. 복잡한 현상들을 간략하고 정확하게 추상화시킴으로써 연구의 폭을 넓히고 정교한 학문적 탐구가 가능해진다.
- 최근에는 오토마타를 이용한 신경망(Neural Networks) 모델링도 시도되고 있으며, 셀룰러 오토마타(Cellular Automata) 등 오토마타를 이용한 여러가지 지능적인 모델링도 연구되고 있다.
2) 유한 상태 시스템 (Finite State Machine : FSM) : 유한개의 상태를 가진 오토마타
; 유한 상태 시스템의 응용 예시
- 엘리베이터의 제어
- 엘리베이터의 제어 방식은 탑승자들이 과거에 요청했던 모든 요구들을 기억하지 않고, 단지 현재의 층수와 엘리베이터의 운동 방향 및 탑승자들이 요청한 것들 중에서 아직까지 이루어지지 않은 요구들만을 기억하고 있는 유한 상태 시스템이다.
- 컴퓨터의 제어 장치와 같은 논리 회로
- 논리 회로는 통상 0과 1로 표시되는 2가지 조건 중 하나의 상태인 유한개의 게이트들의 집합으로 구성된다.
- 따라서 n개의 게이트를 가진 논리 네트워크의 상태는 2n개 중 하나이다.
- 문서 편집기와 어휘분석기
- 문서 편집기(text editor)는 입력을 추가할 때마다 상태가 변화되고, 어휘분석기(lexical analyzer)는 컴퓨터 프로그램에서 심볼들을 차례로 읽어서 문자 스트링들을 변수, 상수, 예약어(reserved word) 등으로 대응시킨다.
- 위의 과정에서 단지 유한개의 정보를 기억하기만 하면 된다.
- 유한 상태 시스템은 오토마타 이론을 적용하여 여러 가지 형태의 스트링들을 효과적으로서 처리하는 데 있어서 매우 유용하다.
13.3 유한 오토마타
1) 유한 오토마타(Finite Automata ; FA)의 기본 개념
- 이산적인 입력과 출력을 가지는 시스템의 수학적 모형이다.
- 유한한 개수의 내부의 상태들을 가지고 있는데, 시스템의 상태는 다음에 들어올 입력에 대한 시스템의 행동을 결정하는데 필요한 과거의 정보들을 요약해서 나타내고 있다.
(1) 인식기로서의 유한 오토마타
- 유한 오토마타의 주요 특징으로는 임시 저장 장치를 가지지 않는다는 점과 입력 테이프는 단지 읽힐 수만 있으며 그 내용이 변경될 수 없다는 점이다.
- 따라서 유한 오토마타의 기능은 작동 과정에서 정보를 기억하느 데 있어서 상당한 제약을 받게 된다.
(2) 유한 제어(finite control)
- 유한 오토마타의 입력과 상태들을 제어한다.
- 유한 오토마타는 여러 종류의 오토마타들 중에서 가장 단순한 형태이다.
2) 유한 오토마타의 구성
- 유한한 상태들의 집합과 전이 함수(transitio function)들의 집합으로 구성된다.
- 전이란 알파벳 Ʃ로부터 선택된 입력 심볼에 의해 생기는, 상태에서 상태로의 변화이다.
- 입력에 따라 상태는 항상 변할 수 있으며, 원래의 상태로 돌아가는 전이도 있을 수 있다.
- 보통 q0(q zero)로 나타내는 상태를 시작 상태(start state)라 하는데, 이 시작 상태에서 오토마타가 시작하게 된다.
- 어떤 상태들은 최종 상태(final state) 또는 인식 상태(accepting state)들로 지정되는데, 그래프에서는 이중의 서클로 표시한다.
- 각 오토마타마다 전이 다이어그램(transition diagram)이라 불리는 방향이 있는 그래프는 아래와 같이 그려진다.
- 전이 다이어그램의 각 노드들은 유한 오토마타의 상태에 해당된다.
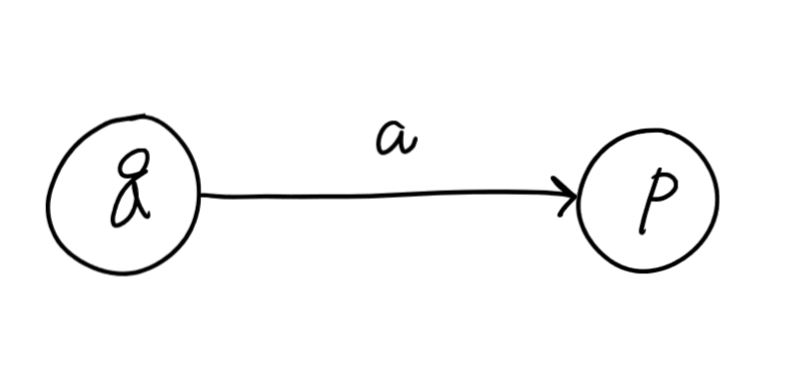
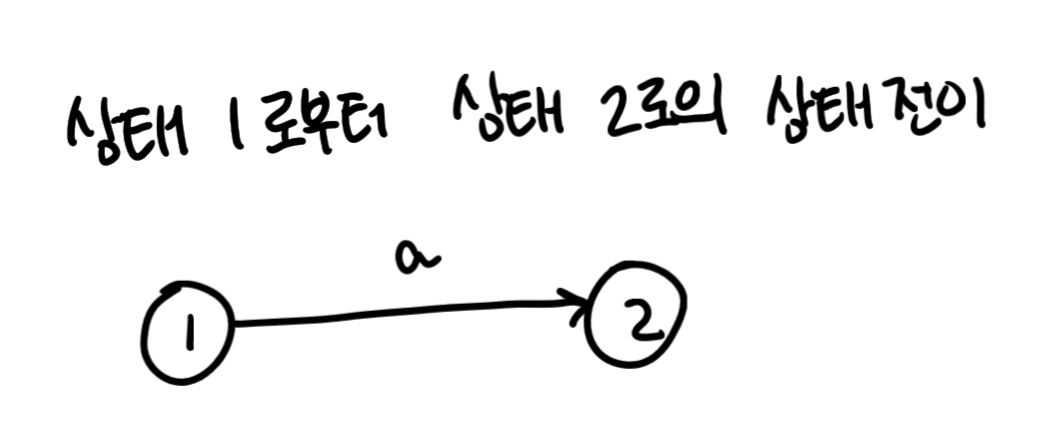
- 어떤 상태 q에서 입력 a를 받아 어느 상태 p로 가는 변환이 있다면 다음과 같다.
- 전이 다이어그램에서는 상태 q에서 상태 p로 가는 연결선이 존재한다.
- 위 연결선의 표식은 a이다.
- 만약 입력 스트링 x에 대해 시작 상태에서 최종 상태로 가는 경로가 존재한다면 유한 오토마타는 스트링 x를 인식하게 된다.
- 유한 오토마타는 전이 방법에 따라 결정적 유한 오토마타와 비결정적 유한 오토마타로 구분되는데, 그 기느엥 있어서는 동치이며 유한 오토마타에 대응되는 언어는 정규 언어(regular language)이다.
3) 결정적 유한 오토마타 (Deterministic Finate Automata : DFA)
- 다음과 같이 5개의 순서쌍으로 이루어진다.

- DFA의 작동 개요
- 처음에는 시작 상태가 q0에 있고 유한 제어는 입력 스트링의 가장 왼쪽에 있는 심볼을 가리킨다.
- 오토마타의 작동에 따라 입력 장치에서 한 심볼씩 오른쪽으로 이동하면서 상태가 바뀐다.
- 스트링을 모두 읽고 난 후 DFA가 최종 상태에 있으면 그 스트링이 '인식되고'(accepted), 그렇지 않으면 기각된다(rejected).
- 스트링이 인식되는 것을 '받아들여진다', 기각되는 것을 '받아들여지지 않는다'고 표현하기도 한다.
- 입력 메커니즘은 왼쪽에서 오른쪽으로의 방향으로만 이동이 가능하며 각 단계에서 하나의 심볼만을 읽을 수 있다.
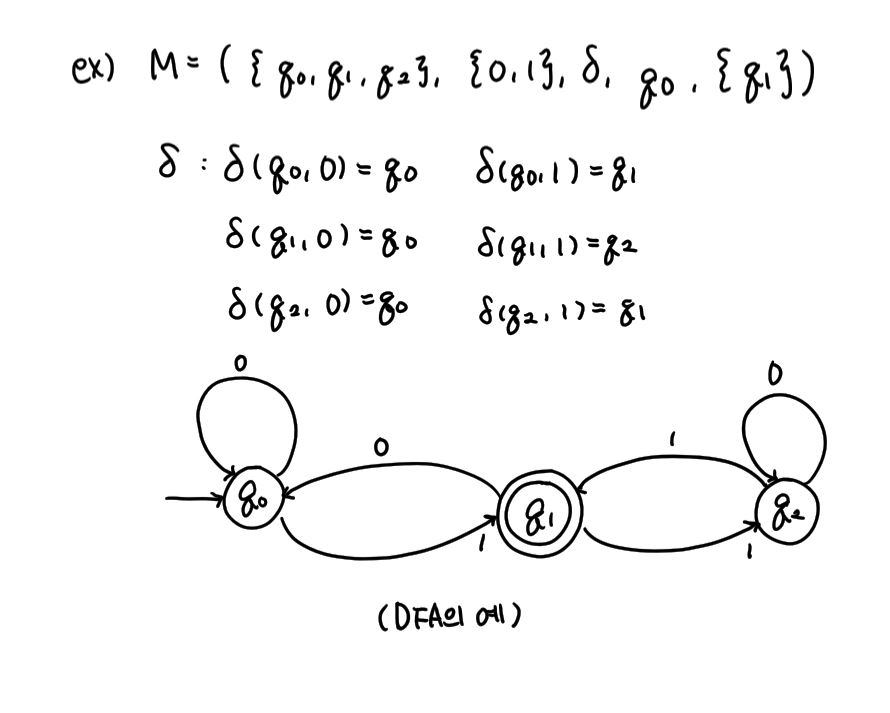
- DFA의 그래프 표현
: 전이 그래프(transition graph)를 사용하게 된다.
- 둥근 원은 상태를나타내고 연결선은 전이를 나타낸다.
- 하나의 DFA에서 |Q|개의 상태가 있으며 어떤 상태 qi ∊ Q 에 대해 δ(qi, a)=qj인 경우 그래프는 a라는 표식의 선(qi, qj)를 가진다.
- 최종 상태인 경우 두 개의 서클로 표시한다.
4) 출력이 없는 유한 오토마타
5) 출력이 있는 유한 오토마타
- 어떤 입력의 개수를 읽는 순간마다 알 수 있는 것이 카운터(counter)란 장치이다.
- 특히 어떤 수를 3으로 나누어서 나머지를 점검하여 출력해내는 오토마타가 Mod-3 오토마타이다.
6) 유한 오토마타의 응용
- 유한 오토마타를 이용하여 변수를 만드는 방법에 대해 알아보자.
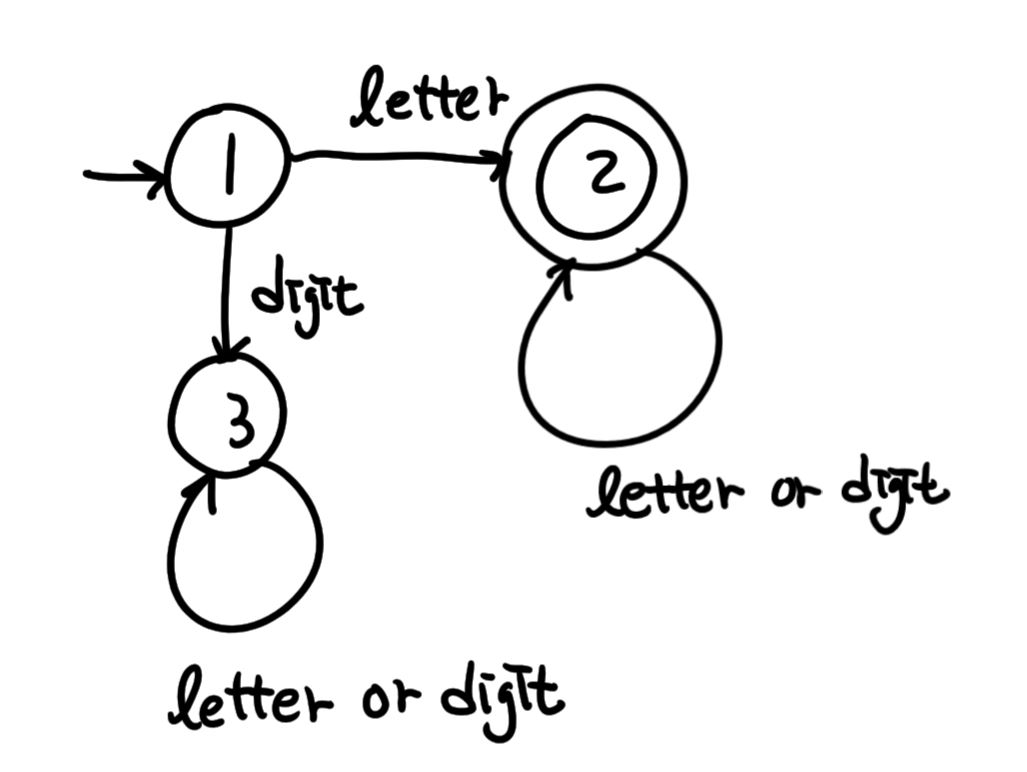
- C언어에 있어서 모든 변수(identifier)들의 집합은 하나의 언어이다.
- 각 변수는 하나의 문자(letter)로 시작되어야 하며, 문자 다음에는 임의 개수의 문자나 숫자(digit)가 혼용하여 사용될 수 있다.

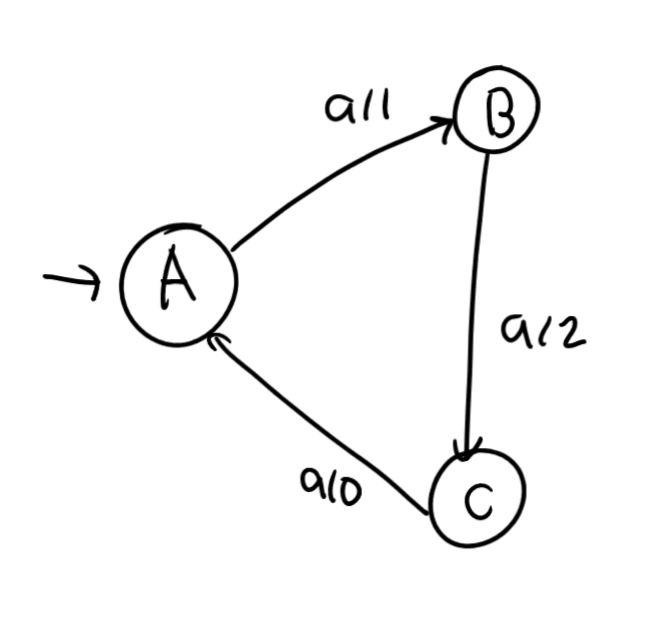
- 입력 a에 의한 상태 전이
- C언어에서의 변수를 인식하는 오토마타
13.4 형식 언어와 문법
1) 형식 언어(formal language)
- 형식 언어는 컴퓨터 관련 학문에 있어서 매우 중요한 역할을 담당해왔다.
- 형식 언어 분야의 연구는 1956년 경 미국의 저명한 언어학자 촘스키(Noam Chomsky)에 의해 시작되었다.
- 그 직후 ALGOL과 같은 컴퓨터 프로그래밍 언어가 개발되었다. ALGOL은 문맥자유 문법(Context-Free Grammer)으로 정의되었다.
- 그 후 이러한 개발은 여러 가지 프로그래밍 언어를 위한 컴파일러에 직접 응용되었다.
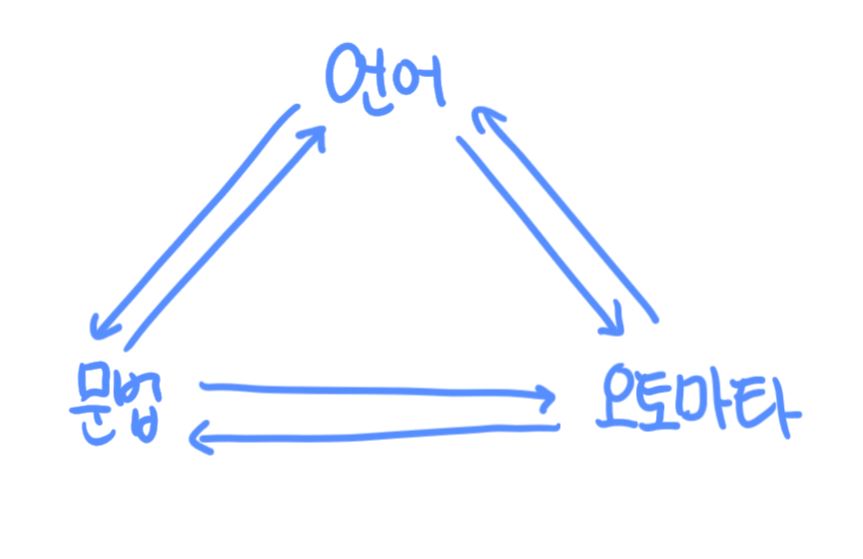
- 오토마타 이론에서 가장 중요한 3가지 개념
- 언어(language)
- 문법(grammer)
- 오토마타(automata)
2) 언어(language)
: 언어는 우리가 일상생활에서 자주 사용하는 자연어(natural language)와 오토마타를 이용하여 만들어지는 이론적인 언어인 형식 언어(formal language)로 구분할 수 있다.
- 알파벳(alphabet)
: 유한개의 공집합이 아닌 심볼들(Symbols)의 집합 Ʃ이며, 이들 심볼들로부터 스트링들(strings)이 만들어지는데, 알파벳으로부터 얻어진 심볼들의 유한개의 시퀀스(sequence)로 이루어진다.
- 팰린드롬(palindromes) : 앞에서부터 읽는 것과 뒤에서부터 읽는 것이 똑같은 스트링들 ex) aba, abba
- 스트링에서의 연산
① 연결 (concatenation)
- 두 개의 스트링 w =a1a2a3...an와 v = b1b2b3...bn를 연결하면 w와 v의 연결 wv = a1a2a3...anb1b2b3...bn이다.
② 역 (reverse)
- 어떤 스트링의 역은 주어진 심볼들을 거꾸로 나열한 것이다.
- w=a1a2a3...an이라면 그것의 역인 wR은 wR=an...a2a1이 된다.
③ 스트링의 길이
- 스트링의 길이는 스트링에 포함된 심볼의 개수를 말하는데 |w|와 같이 나타낸다.
- 만일 주어진 스트링이 어떠한 심볼도 가지고 있지 않다면 공스트링(empty string)이라 하고 통상 λ로 나타낸다.
- |λ|=0, 모든 w에 대해 λw = wλ = w가 성립한다.
④ 스트링의 반복
- w가 스트링일 때 wn이란 w를 n번 연결한 것이다.
- 모든 w에 대해 w0 = λ가 된다.
⑤ Ʃ*와 Ʃ+
- Ʃ가 알파벳일 때 Ʃ*는 Ʃ상에서의 심볼들의 결합으로부터 만들어지는 모든 스트링들의 집합이다.
- 이때 Ʃ*는 λ를 항상 포함한다.
- Ʃ*에서 λ를 제외할 경우에는 Ʃ+로 표현한다.
⑥ 언어와 문장
- 언어란 일반적으로 Ʃ*의 부분 집합으로 정의되는데 통상 대문자로 표현된다.
- 언어 L 안에 있는 어떤 스트링 w는 L의 단어(word) 또는 문장(sentence)으로 불린다.
⑦ 언어에서의 연산
- 언어는 단어들로 이루어진 집합이므로 합집합, 교집합, 차집합 등 집합의 일반적인 연산이 가능하다.
- 여집합, 연결 등의 연산도 가능하다.
3) 문법(grammer)
- 일반적으로 문법이란 우리가 사용하는 자연어에서의 문법을 일컫는데, 컴퓨터에서 쓰이는 문법에는 애매성이 배제되어야 하며 일정한 규칙을 따라 엄밀하게 정의되어야 한다.
- 컴퓨터에서 사용되는 문법은 배커스와 나우어에 의해 체계화된 배커스-나우어 표기법(Backus-Naur : BNF)과 푸시다운 오토마타(Push-Down Automata : PDA)에 의한 문맥자유 문법(Context-Free Grammer : CFG)으로 구별될 수 있다. (표현 방법은 다르지만 기능상에서의 차이는 없다.)
- 문법 G의 정의
G = (N, T, P, S)
N : 변수(variable)라고 불리는 넌터미널 심볼(nonterminal symbol)들의 유한집합, 통상 대문자 알파벳으로 표현한다.
T : 터미널 심볼(terminal symbol)의 유한집합, 통상 소문자 알파벳으로 표현한다.
P : 생성 규칙 (production rule)의 유한 집합. 집합 P는 A→X1X2...Xn와 같이 표현된다. (A는 넌터미널, X1X2...Xn은 유한한 길이의 터미널 또는 넌터미널 심볼이다.)
S : N에 속하는 시작 심볼(start symbol)로서 문장의 시작을 나타내며 통상 S를 사용한다.
- ⇒는 유도된다(derived)라고 말하는데 w⇒z일 때 'w는 z를 유도한다' 또는 'z는 w로부터 유도된다'라고 표현된다.


- 두 개의 문법 G1, G2가 똑같은 언어 L를 생성할 때 G1과 G2는 동치(equivalent)라고 한다.
13.5 튜링 머신 모델
1) 효과적인 프로시저(procedure)를 수행할 수 있는 모델의 조건
- 각 프로시저는 유한하게 기술될 수 있어야 한다.
- 프로시저는 기계적으로 수행되는 이산적인 단계들로 이루어져야 한다.
2) 튜링머신
- 효과적인 프로시저를 수행할 수 있는 모델의 조건을 만족하는 최초의 모델
- 1936년 영국의 수학자인 튜링(Turing)에 의해 만들어졌다.
- 튜링머신 M은 다음과 같은 7개의 쌍으로 정의된다.
M = (Ǫ, Ʃ, Γ, δ, q0, B, F)
Ǫ : 상태들의 유한 집합
Γ : 허용되는 테이프 심볼들의 유한 집합
B : Γ에 속하는 블랭크(blank)
Ʃ : 입력 심볼의 집합으로서 B를 포함하지 않으며 Γ의 부분 집합
δ : 다음 동작 함수 (next move function)인데, Ǫ×Γ→Ǫ×Γ×{L, R}이다. (여기서 δ는 경우에 따라 정의되지 않을 수도 있다. 여기서 L과 R은 각각 왼쪽과 오른쪽으로의 이동을 의미한다.)
q0 : 시작상태로서 q0∊Q이다.
F : F ⊆ Q은 최종 상태의 집합
- 튜링머신을 단 하나의 일차원적 셀들의 배열인 테이프(tape)를 가진 것으로 생각할 수 있다.
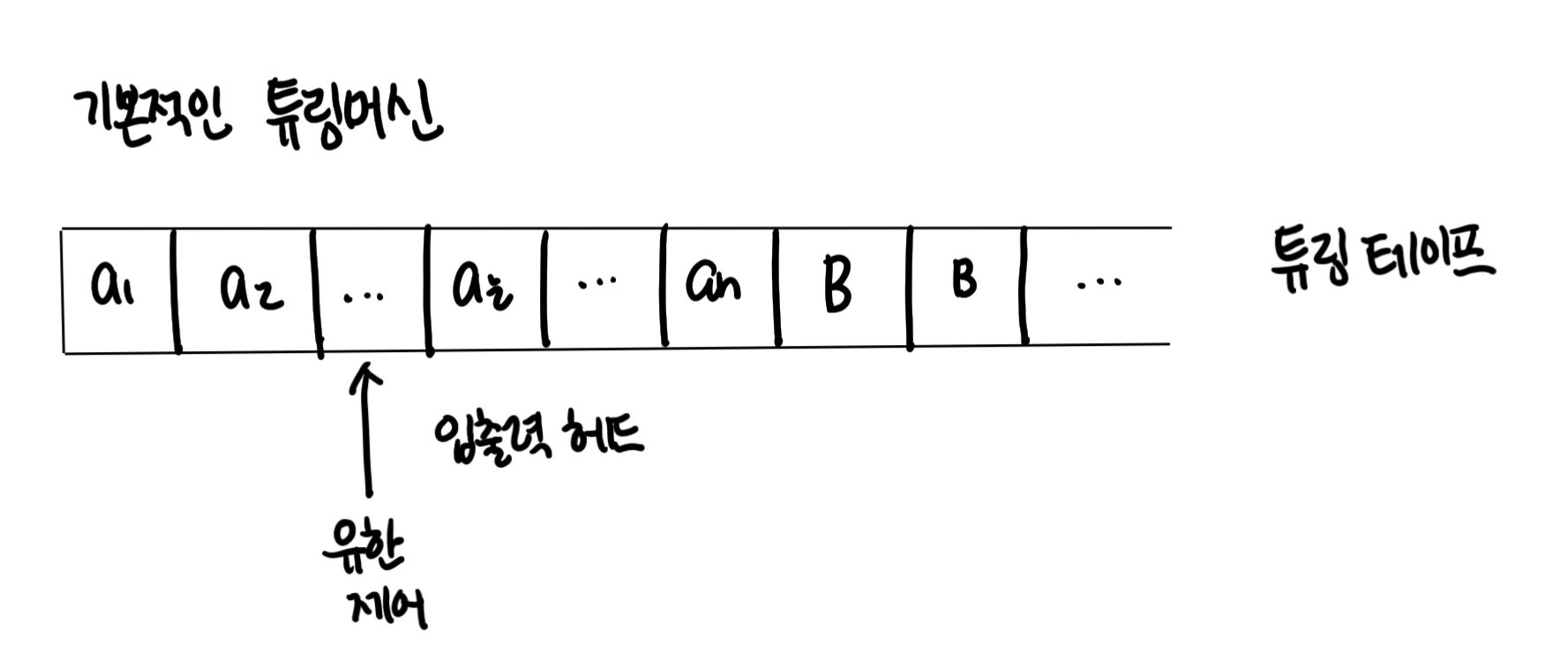
- 이 테이프는 양방향으로 무한정 확장이 가능하기 때문에 저장할 수 있는 정보의 양이 무한하다.
- 각 셀에 저장된 정보는 어떤 순서로든 읽거나 수정이 가능하다.
- 튜링머신은 그것의 임시 기억 장치가 테이프인 오토마타이다.
- 테이프는 셀들로 나누어져 있는데 각 셀은 하나씩의 심볼을 가진다.
- 테이프의 왼쪽이나 오른쪽을 이동하면서 각 동작마다 하나의 심볼을 읽고 하나의 심볼을 쓰는 입출력 헤드(read-write head)가 존재하며 제어 유니트의 명령에 따라 동작하게 된다.
- 튜링머신 M에 의해 인식되는 언어인 L(M)은 M의 테이프 헤드가 가장 왼쪽 셀에 위치하고, q0 상태에서 시작하여 M이 최종 상태에 들어가게 하는 Ʃ* 내의 단어들의 집합이다.
- L(M) = {w ∊ Ʃ* | q0w ├ a1 p a2 for some p ∊ F and a1,a2 ∊ Γ*}
- 어떤 튜링머신 M이 언어 L을 인식하게 된다는 것은 튜링머신의 상태가 최종 상태에 들어가면서 정지하는 경우이다. (인식되지 않을 때에는 튜링머신이 정지하지 않을 수 있다.)
13.6 촘스키 포함 관계
촘스키 포함 관계
- 형식 언어의 선구자 촘스키는 4가지 문법의 패밀리에 숫자를 붙여서 포함된 관계를 나타냈다.
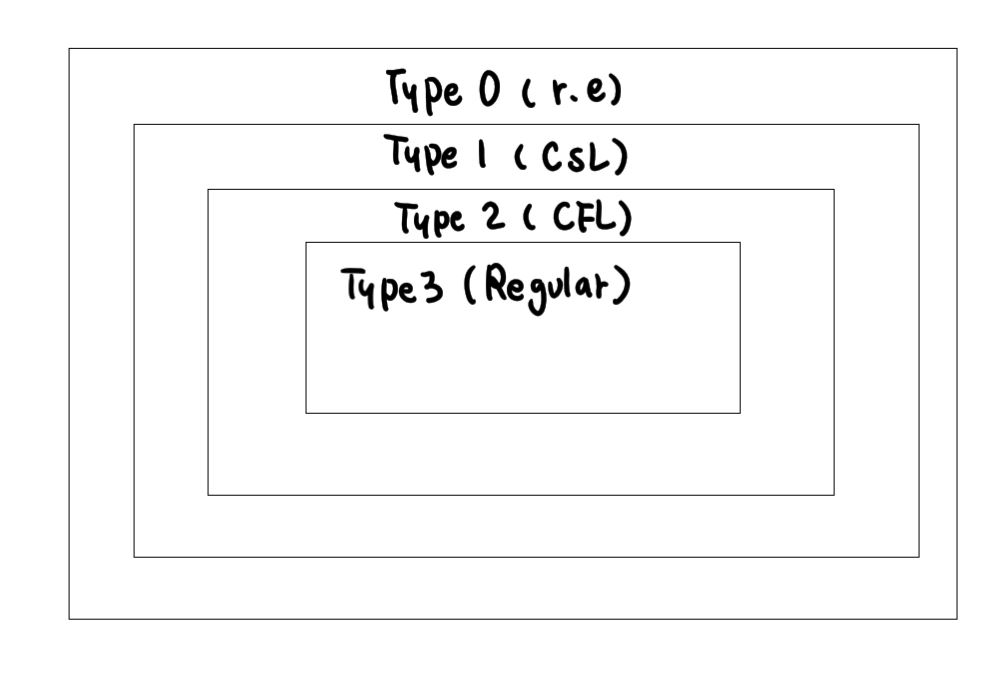
- 무제한 문법, 문맥민감 문법, 문맥자유 문법, 정규 문법을 각각 type 0, type 1, type 2, type3 문법으로 명명하였는데, 문법의 숫자가 커질수록 제한이 많아진다.
- 문법의 포함관계는 해당 언어들의 포함관계로 이어져서 소위 촘스키 포함 관계를 형성한다.
- 정규 언어는 CFL(Context-Free Language)의 진부분 집합이다.
- 공스트링이 아닌 CFL은 CSL(Context-Sensitive Language)의 진부분 집합이다.
- CSL은 r. e(recursively enumerable) 언어의 진부분 집합이다.
- 모든 type i 언어는 type (i-1) 언어에 속한다.
| 문법 | 언어 | 오토마타 |
| Type 0 (무제한 문법) | r. e Language | 튜링머신 |
| Type 1 (문맥민감 문법) | CSL | 선형제한 오토마타 |
| Type 2 (문맥자유 문법) | CFL | 푸시다운 오토마타 |
| Type 3 (정규 문법) | Regular Language | 유한 오토마타 |
13.7 오토마타의 응용과 4차 산업혁명과의 관계
1) 오토마타 응용의 다양한 분야들
- 오토마타의 간단한 응용으로는 물시계와 모래시계 등을 들 수 있다.
- 오토마타 원리는 엘리베이터 제어, 디지털 디자인, 논리 제어, 시스템 설계, 신경생리학, 통신, 신경망, 언어론 등 다양한 분야에 직접 활용되고 있다.
2) 컴퓨터 관련 분야의 응용들
- 오토마타는 디지털 컴퓨터의 추상적 모델로서 디지털 컴퓨터가 작동하는 이론적인 메커니즘이라 볼 수 있다.
- 각종 프로그래밍 언어도 오토마타 원리에 의해 만들어졌으며, 그것을 번역하는 컴파일러(Compiler)도 오토마타의 주요 응용 영역에 속한다.
3) 오토마타와 4차 산업혁명과의 관계 : 광 컴퓨터
- 광 컴퓨터(Optical computer)는 광 신호로 작동하는 논리 소자를 이용한 신호를 통하여 빛에 의해 연산하는 컴퓨터를 말한다.
- 광 컴퓨터는 광 재료 및 디바이스, 기억소자, 상호 연결된 네트워크 등에서 오토마타에 의해 정교하여 제어되어야 하므로 오토마타의 역할과 응용이 특히 필요한 분야이다.
'전공과목 정리 > 이산수학' 카테고리의 다른 글
| [이산수학🔗] 알고리즘을 통한 문제 해결 (12장) (0) | 2023.01.19 |
|---|---|
| [이산수학🔗] 부울 대수 (11장) (0) | 2023.01.18 |
| [이산수학🔗] 행렬과 행렬식 (10장) (2) | 2023.01.15 |
| [이산수학🔗] 순열, 이산적 확률, 재귀적 관계 (9장) (0) | 2023.01.13 |
| [이산수학🔗] 트리 (8장) (2) | 2023.01.13 |