포스팅에 참고하는 교재 : 4차 산업혁명 시대의 이산수학 개정판 (생능출판)
8.1 트리의 기본 개념
1) 트리(Tree)
- 그래프 모양이 나무를 거꾸로 세워놓은 것처럼 생겼다고 해서 붙여진 이름. 수형도라고도 한다.
- 그래프의 특별한 형태로서 컴퓨터를 통한 자료 처리와 응용에 있어서 매우 중요한 역할을 담당한다.
- 이진 트리의 경우에는 산술적 표현이나 자료 구조 등을 매우 간단하게 표현할 수 있는 장점이 있다.
- 하나 이상의 노드(node)로 구성된 유한 집합으로서 다음의 2가지 조건을 만족한다.
- 특별히 지정된 노드인 루트(root)가 있다.
- 나머지 노드들은 다시 각각 트리이민셔 연결되지 않는(disjoint) T1, T2, ... , Tn (n ≥ 0)으로 나누어진다. 이때 T1, T2, ... , Tn을 루트의 서브트리(subtree)라고 한다.

- n개의 노드를 가진 트리는 n-1개의 연결선을 가진다.
- 그래프 G = (V, E)에서 |V| = n이고 |E|=m일 때 다음의 문장들은 모두 동치이다.
- G는 트리이다.
- G는 연결되어 있고 m=n-1이다.
- G는 연결되어 있고 어느 한 연결선만을 제거하더라도 G는 연결되지 않는다.
- G는 사이클을 가지지 않으며 m = n-1이다.
- G는 어느 한 연결선만 첨가하더라도 사이클을 형성하게 된다.
- n-트리(n-ary tree)
- 트리 T가 n-트리란 말은 모든 중간 노드들이 최대 n개의 자식 노드를 가질 때를 말한다.
- n이 2인 경우를 이진트리(binary tree)라고 한다.
2) 트리에서 사용되는 용어
- 루트(root) : 주어진 그래프의 시작 노드로서 통상 트리의 가장 높은 곳에 위치한다.
- 차수(degree) : 어떤 노드의 차수는 그 노드의 서브 트리의 개수를 나타낸다.
- 잎 노드(leaf node) : 차수가 0인 노드
- 자식 노드(children node) : 어떤 노드의 서브 트리의 루트 노드들
- 부모 노드(parent node) : 자식 노드의 반대 개념
- 형제 노드(sibling node) : 동일한 부모를 가지는 노드
- 중간 노드(internal node) : 루트도 아니고 잎 노드도 아닌 노드
- 조상(ancestor) : 루트로부터 그 노드에 이르는 경로에 나타난 모든 노드들
- 자손(descendant) : 그 노드로부터 잎 노드에 이르는 경로상에 나타난 모든 노드들
- 레벨(level) : 루트의 레벨을 0으로 놓고 자손 노드로 내려가면서 하나씩 증가한다.
- 트리의 높이(height) : 트리에서 노드가 가질 수 있는 최대 레벨. 트리의 깊이(depth)라고도 한다.
- 숲(forest) : 서로 연결되지 않은 트리들의 집합. 트리에서 루트를 제거하면 얻을 수 있다.
8.2 방향 트리
; 방향이 있고 순서화된 트리는 다음의 성질들을 만족하는 방향 그래프이다.
- 선행자가 없는 루트라고 불리는 노드가 하나 있으나, 이 루트에서는 모든 노드로 갈 수 있는 경로가 있다.
- 루트를 제외한 모든 노드들은 오직 하나씩만의 선행자를 가진다.
- 각 노드의 후속자들은 통상 왼쪽으로부터 순서화된다.
- 어떤 방향 트리를 그릴 때 그 트리의 루트는 가장 위에 있다.
- 아크(연결선)들은 밑을 향하여 그려진다.
8.3 이진 트리
1) 이진 트리 (binary tree)
: 노드들의 유한 집합으로서, 공집합이거나 루트와 왼쪽 서브 트리, 오른쪽 서브 트리로 이루어진다.
- 이진 트리가 레벨 i에서 가질 수 있는 최대한의노드 수는 2^i개이다.
- 높이가 k인 이진 트리가 가질 수 있는 최대한의 전체 노드 수는 2^(k+1)-1이다.
- 이진 트리에서 잎 노드의 개수를 n0, 차수가 2인 노드의 개수를 n2라고 할 때 n0 = n2+1의 식이 항상 성립한다.
2) 이진 트리의 종류
- 사향 이진 트리 (skewed binary tree)
: 왼쪽 또는 오른쪽으로 편향된 트리의 구조를 가진다.
- 완전 이진 트리 (complete binary tree)
: 높이가 k일 때 레벨 1부터 k-1까지는 모두 차 있고 레벨 k에서는 왼쪽 노드부터 차례로 차 있는 이진 트리이다.
- 포화 이진 트리 (full binary tree)
: 잎 노드가 아닌 것들은 모두 2개씩의 자식 노드를 가지며 트리의 높이가 일정한 경우를 말한다.

8.4 이진 트리의 표현
- 이진 트리를 표현하는 방법
- 배열(array)에 의한 방법과 연결 리스트(linkede list)에 의한 방법으로 나눌 수 있다.
- 배열에 의한 방법은 트리의 중간에 새로운 노드를 삽입하거나 기존의 노드를 지울 경우 비효율적이다.
- 일반적으로 가장 많이 쓰이고 있는 방법은 연결 리스트에 의한 방법이다.
- 연결 리스트에 의한 표현
: 데이터(data)를 저장하는 중간 부분, 왼쪽 자식(left child), 오른쪽 자식(right child)을 각각 가리키는 포인터(pointer) 부분으로 구성된다.
typedef struct treenode{
struct treenode *leftchild;
char data;
struct treenode *rightchild;
} TREE;
8.5 이진 트리의 탐방
1) 이진 트리의 탐방
- 트리는 자료의 저장과 검색에 있어서 매우 중요한 구조를 제공한다.
- 트리에서의 연산에는 여러 가지가 있으나 가장 빈번하게 하는 것은 각 노드를 한 번씩만 방문하는 탐방(traversal)일 것이다.
- 탐방의 결과, 각 노드에 들어 있는 데이터를 차례로 나열하게 된다.
- 이진 트리를 탐방하는 것은 여러가지 응용에 널리 쓰인다.
- 각 노드와 그것의 서브트리를 같은 방법으로 탐방할 수 있다.
- 왼쪽(left)으로의 이동을 L, 데이터(data)의 출력을 D, 오른쪽(right)으로의 이동을 R로 나타내고, 왼쪽을 항상 오른쪽보다 먼저 방문한다고 가정하면 LDR, DLR, LRD의 3가지 경우가 있다.
- LDR는 중순위 표기(infix), DLR은 전순위 표기(prefix), LRD는 후순위 표기(postfix)와 각각 대응된다.
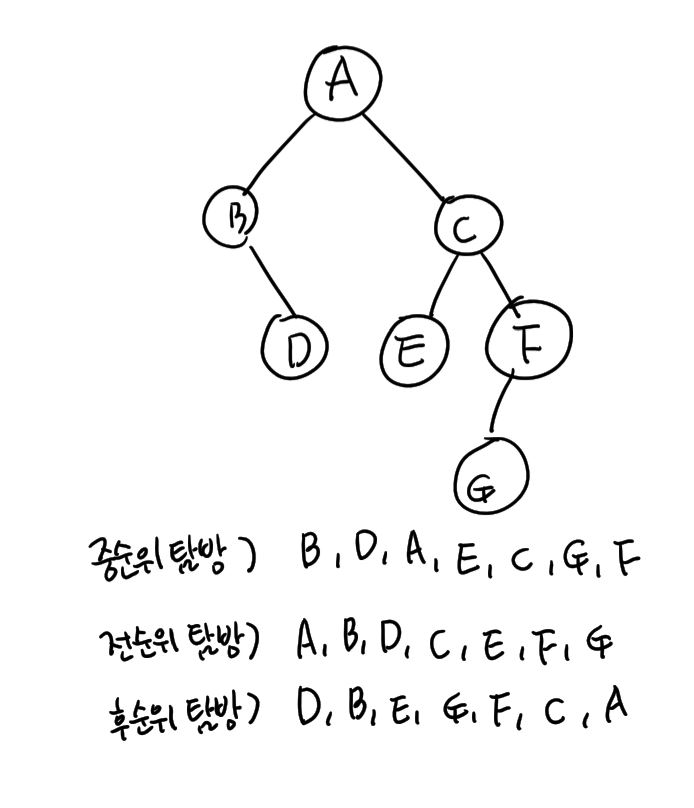
2) 중순위 탐방 (inorder traversal)
- 루트에서 시작하여 트리의 각 노드에 대하여 다음과 같은 재귀적(recursive) 방법으로 정의된다.
- 트리의 왼쪽 서브 트리를 탐방한다.
- 노드를 방문하고 데이터를 프린트한다.
- 트리의 오른쪽 서브 트리를 탐방한다.
void inorder(TREE *currentnode)
{
if (currentnode != NULL)
{
inorder(currentnode->leftchild);
printf("%c", currentnode->data);
inorder(currentnode->rightchild);
}
}
3) 전순위 탐방 (preorder traversal)
- 루트에서 시작하여 트리의 각 노드에 대하여 다음과 같은 재귀적(recursive) 방법으로 정의된다.
- 노드를 방문하고 데이터를 프린트한다.
- 트리의 왼쪽 서브 트리를 탐방한다.
- 트리의 오른쪽 서브 트리를 탐방한다.
void preorder(TREE *currentnode)
{
if (currentnode != NULL)
{
printf("%c", currentnode->data);
preorder(currentnode->leftchild);
preorder(currentnode->rightchild);
}
}
4) 후순위 탐방 (postorder traversal)
- 루트에서 시작하여 트리의 각 노드에 대하여 다음과 같은 재귀적(recursive) 방법으로 정의된다.
- 트리의 왼쪽 서브 트리를 탐방한다.
- 트리의 오른쪽 서브 트리를 탐방한다.
- 노드를 방문하고 데이터를 프린트한다.
void postorder(TREE *currentnode)
{
if (currentnode != NULL)
{
postorder(currentnode->leftchild);
postorder(currentnode->rightchild);
printf("%c", currentnode->data);
}
}
8.6 생성 트리와 최소비용 생성 트리
1) 생성 트리(spanning tree)
: 어떤 그래프 G에서 모든 노드들을 포함하는 트리
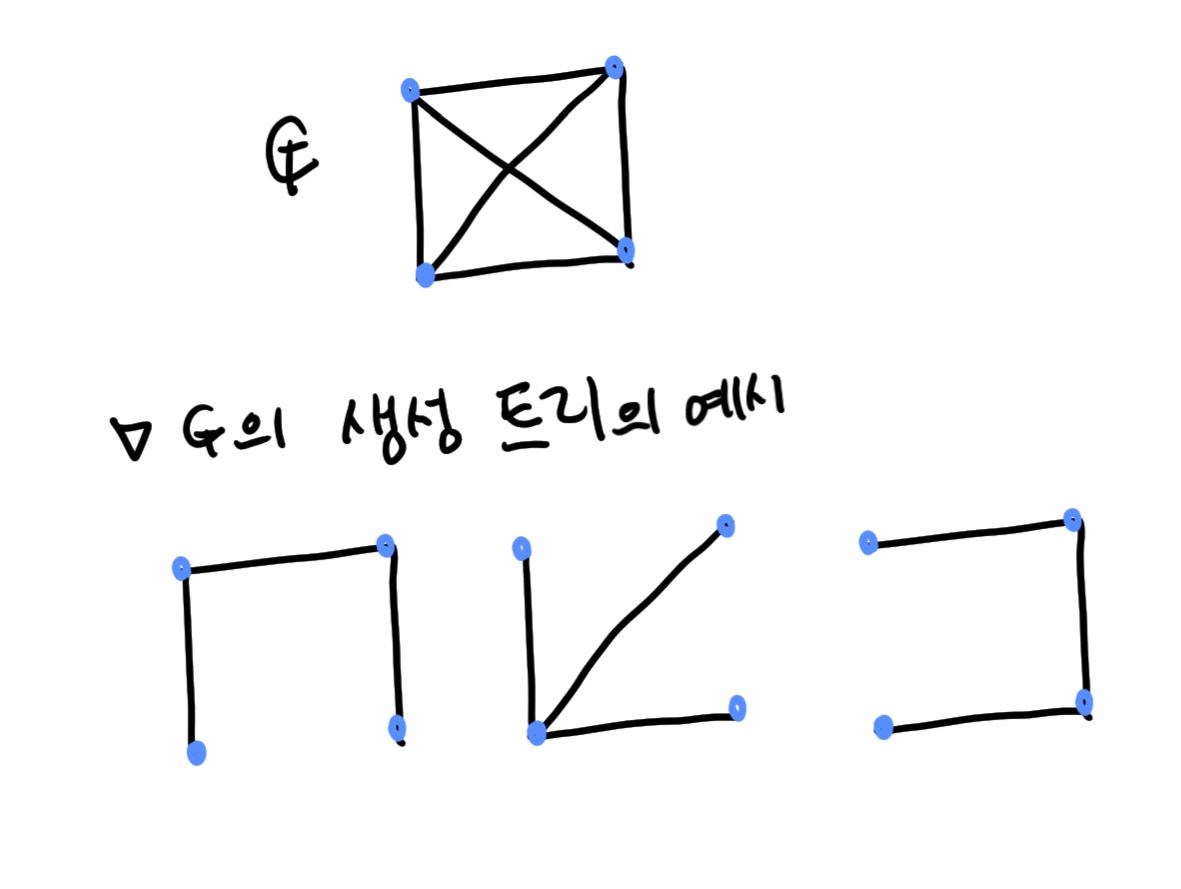
2) 최소 비용 생성 트리 (Minimum Spanning Tree ; MST)
- 생성 트리의 비용(cost)은 트리 연결선의 값을 모두 합한 값이다.
- 최소 비용 생성 트리는 최소한의 비용을 가지는 생성 트리를 말한다.
- 최소 비용 생성 트리의 대표적인 예는 통신 네트워크의 연결이다.
- 최소 비용 생성 트리의 대표적인 2가지 방법은 프림(Prim)의 알고리즘과 크루스칼(Kruskal)의 알고리즘이다.
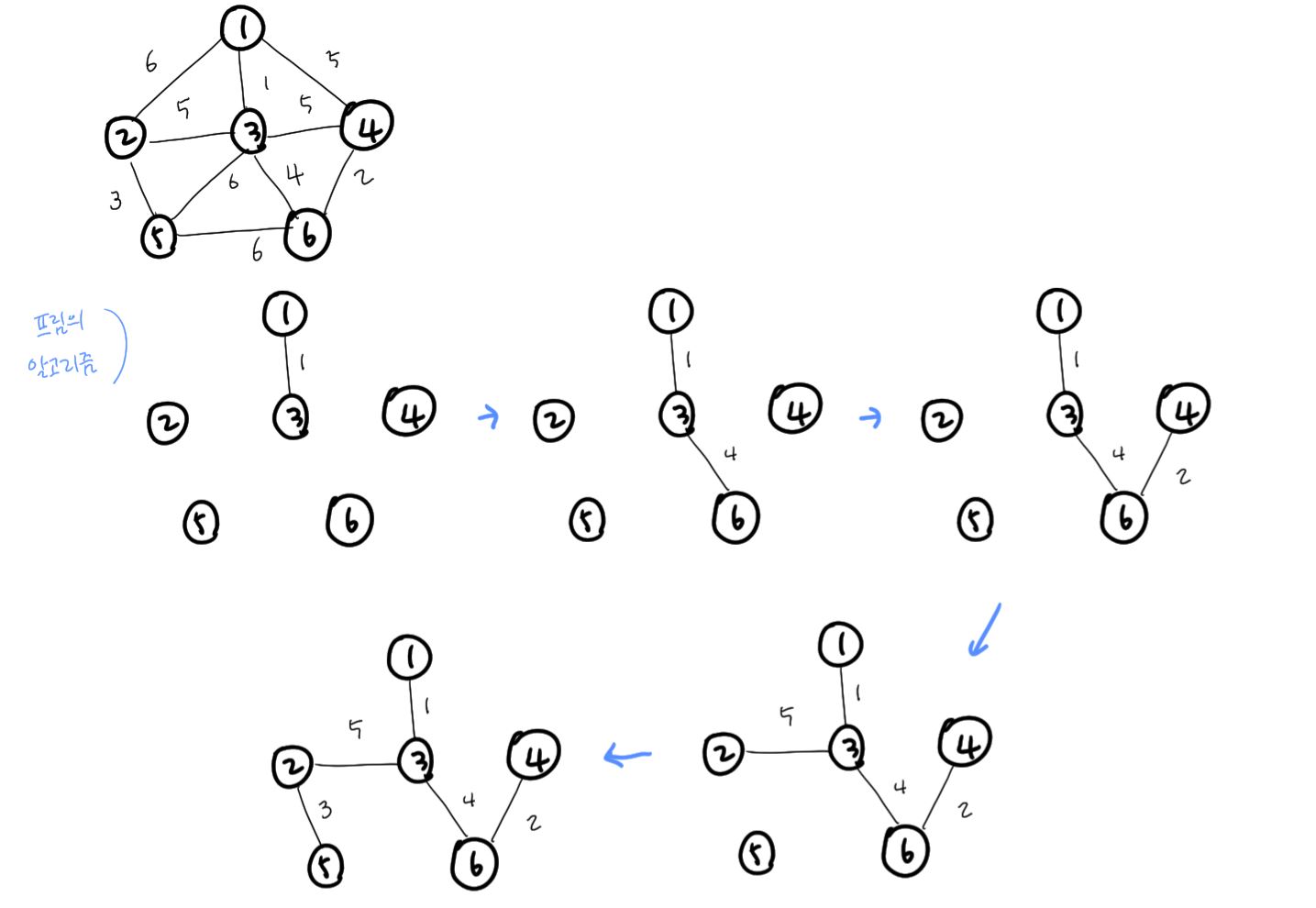
- 프림의 알고리즘 (Prim's algorithm)
- 주어진 가중 그래프 G = (V, E)에서 V = {1, 2, ..., n}이라고 하자.
- 노드의 집합 U를 1로 시작한다.
- u∊U, v∊V-U일 때 U와 V-U을 연결하는 가장 짧은 연결선인 (u,v)를 찾아서 v를 U에 포함시킨다. 이때 (u,v)는 사이클(cycle)을 형성하지 않는 것이어야 한다.
- 위의 과정을 U = V일 때까지 반복한다.
void Prim(graph G:set_of_edges T)
{
set_of_vertices U;
vertex u,v;
T = NULL;
U = {1};
while (U != V)
{
let (u,v) be a lowest cost edge such that u is in U and v is in V-U;
T = T∪{(u,v)};
U = U∪{v};
}
}
- 크루스칼의 알고리즘 (Kruskal's algorithm)
- 주어진 가중 그래프 G = (V, E)에서 V = {1, 2, ..., n}이라고 하고 T를 연결선의 집합이라고 하자.
- T를 ∅으로 놓는다.
- 연결선의 집합 E를 비용이 적은 순서로 정렬한다.
- 가장 최솟값을 가진 연결선 (u,v)를 찾아서 (u,v)가 사이클을 이루지 않으면 (u,v)를 T에 포함시킨다.
- 위의 과정을 |T|=|V|-1일 때까지 반복한다.
// 연결선의 집합을 정렬한 후
T = NULL;
while (T contains less than n-1 edges and E not empty)
{
choose an edge (v, w) from E of lowest cost;
delete (v, w) from E;
if ((v,w) does not create a cycle in T) add (v,w) to T;
else discard (v,w);
}
if (T contains fewer than n-1 edges) printf("no spanning tree\n");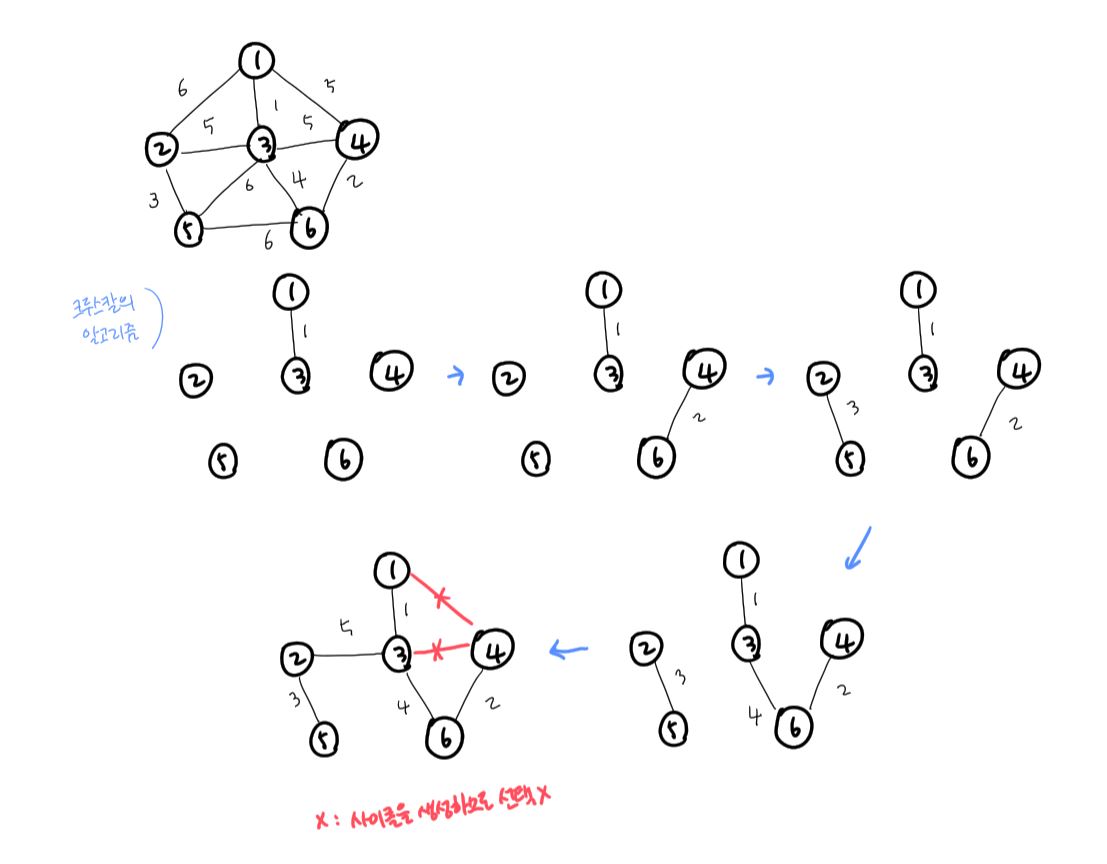
8.7 트리의 활용
1) 문법의 파싱 (parsing)
- 트리는 문법의 파싱을 통하여 자연어 처리와 컴파일러(compiler) 등에 활용됨.
- 문장 트리에서 문장은 주어, 동사, 목적어로 이루어짐.
- 주어는 관사와 명사구로 나누어지고 목적어는 관사와 명사구로 나누어짐.
- 명사구는 형용사와 명사로 다시 나누어지는 파싱 과정을 반복한다.
2) 허프만 코드 (Huffman code)
- 알파벳의 열(sequence)로서 이루어진 메시지가 있고, 각 메시지의 영문자가 각각 독립적이고 위치에 관계없이 어떤 정해진 확률로 나타남.
- 영문자들을 각각 코드화할 때, 어느 영문자의 코드도 다른 어떤 영문자의 코드의 접두어로 표현되어서는 안 된다.
- 허프만 코드 특성을 이용하여 최소 개이 코드로써 정확하게 송신할 수 있으며, 수신된 코드를 정확하게 코드화할 수 있다.
- 허프만 알고리즘은 접두어 성질을 만족하는 최적의 코드화 방법
; 자주 나타나는 문자는 코드 길이가 짧아지고, 잘 나타나지 않는 문자는 코드 길이가 커진다.
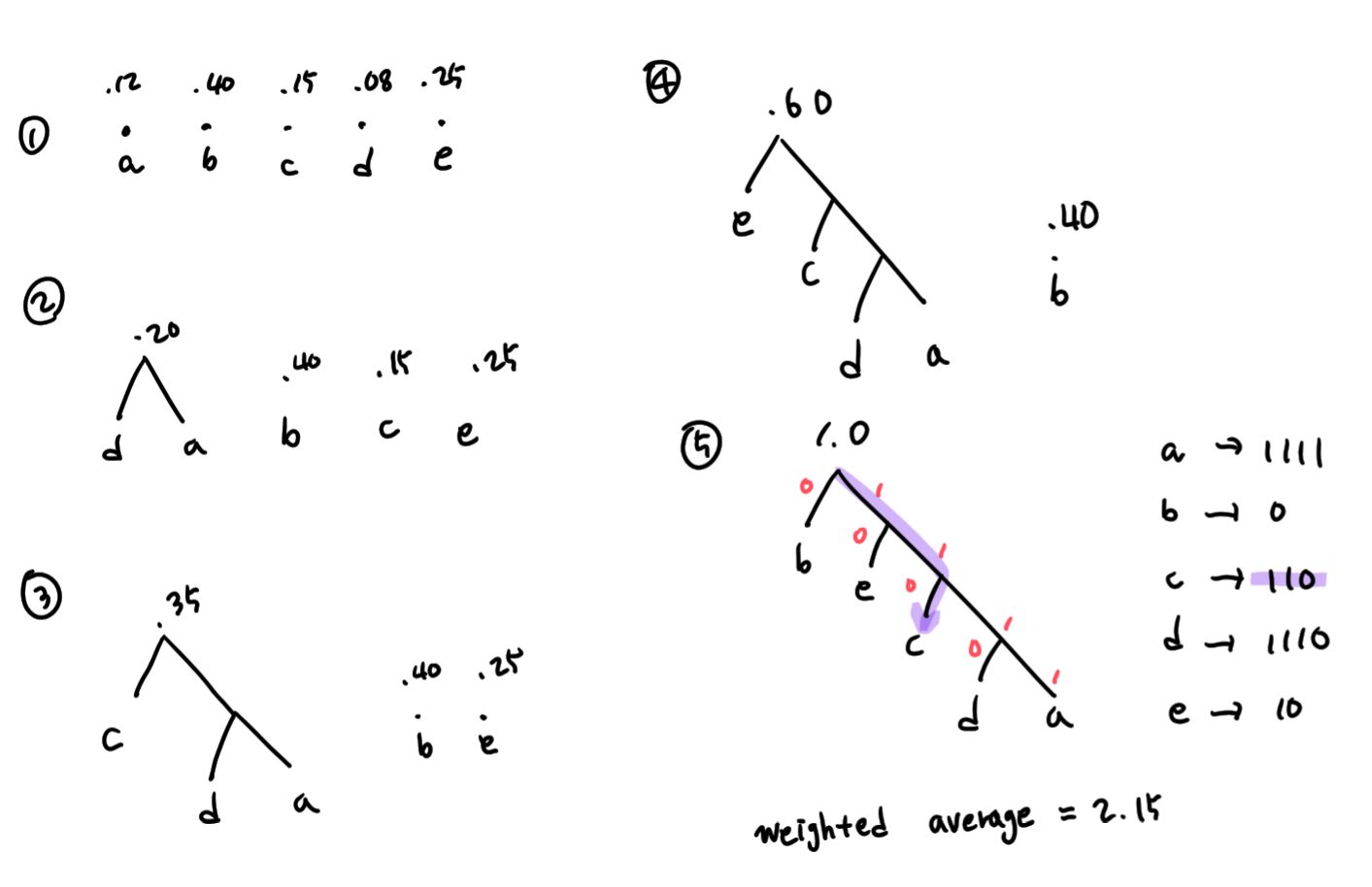
- 허프만 알고리즘 (Huffman algorithm)
- 가장 낮은 확률을 가진 두 문자 a, b를 선택하여 가상이 다른 문자 x로 대치한다. x가 나타날 확률은 a와 b의 확률을 각각 더한 것이다.
- 위의 과정을 반복하여 최종 확률이 1이 될 때까지 계속한다.
- 최종적인 트리가 완성되면 각 서브 트리의 왼쪽에는 0을 부여하고 오른쪽에서 1을 각각 부여하여 각 문자의 코드를 결정한다.
[IT개론] 데이터 표현과 디지털 논리
내용 출처 : 소프트웨어 세상을 여는 컴퓨터과학 1. 수의 체계와 변환 1) 수의 체계 (1) 진법 : 사용할 수 있는 숫자의 개수와 각 숫자의 위치값을 정의한 수 체계 (2) 진법의 종류 : 10진법, 2진법, 8
0yeonjae2.tistory.com
3) 결정 트리
- 트리를 이용할 때 매우 유용하게 쓰인다.
- 가능성 있는 경우의 수가 너무나 많기 때문에 모든 면에서 입증하기가 매우 어려운 문제를 만날 수 있다.
- 결정 트리를 활용하면 주어진 문제를 일목요연하게 입증할 수 있다.
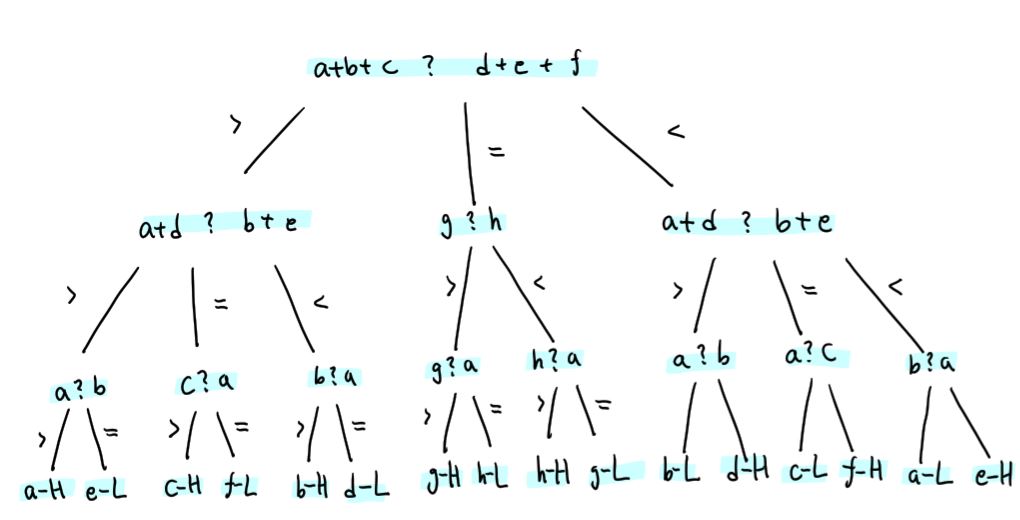
(1) 8개의 동전 문제 (eight-coins problem)
- 결정 트리의 예로 잘 알려져 있다.
- 크기와 색깔이 똑같은 8개의 동전 a,b,c,d,e,f,g,h 중에서 한 개는 불량품이라서 다른 동전들과는 다른 무게를 가진다.
- 무게가 같거나 크고 작은 것만을 판단할 수 있는 하나의 천칭 저울을 사용하여 단 세 번만의 계량으로 어느 동전이 불량품이고, 다른 동전보다 무겁거나 가벼운지를 동시에 판단하고자 한다.
void comp(int x, int y, int z) // x를 정상품인 z와 비교한다.
{
if (x>z) printf("%d is heavy \n", x);
else printf("%d is light \n", y);
}
void eight-coins()
{
int a,b,c,d,e,f,g,h;
scanf("%d %d %d %d %d %d %d %d", &a, &b, &c, &d, &e, &f, &g, &h);
switch(compare(a+b+c, d+e+f))
{
case '=': if (g>h) comp(g,h,a);
else comp(h,g,a);
break;
case '>': switch(compare(a+d, b+e))
{
case '=':comp(c,f,a);
case '>':comp(a,e,b);
case '<':comp(b,d,a);
}
break;
case '<': switch(compare(a+d, b+e))
{
case '=':comp(f,c,a);
case '>':comp(d,b,a);
case '<':comp(e,a,b);
}
break;
}
}
4) 게임
- 트리는 체스, 틱텍토(tic-tac-toe), 장기, 바둑 등 게임에 있어서의 진행과 전략을 구사할 수 있는 게임 트리로도 활용된다.
- 게임 트리를 이용하는 또 다른 응용으로는 인공지능 문제를 해결하는 8-puzzle 게임이 있다.
8.8 트리의 응용과 4차 산업혁명과의 관계
1) 트리의 응용 분야
(1) 복잡한 문제 분석과 다양한 학문 분야에서의 응용
- 트리 구조의 가장 큰 역할은 트리를 통해 복잡한 경우의 수를 명확히 분류할 수 있다는 점이다.
- 트리는 전기회로망 설계와 응용, DNA 구성과 관련된 유전학, 화학 결합에서의 분자구조식 설계, 복잡한 사회 현상 규명을 위한 사회 과학 등에 폭넓게 응용되고 있다.
(2) 컴퓨터 관련 문제 해결에의 응용
: 트리는 컴퓨터 관련 논제 중 데이터베이스의 구성, 최적화 문제의 해결, 통신 네트워크, 문법의 파싱, 언어들 간의 번역, 자료의 탐색, 결정 트리, 게임 등에 매우 유용하게 응용되고 있다.
2) 트리와 4차 산업혁명과의 관계 : 인공지능
- 트리는 인공지능에 있어서의 효율적인 탐색 기법을 제공한다.
- 게임에 있어서의 인공지능적인 탐색이나 최단 경로 찾기 등에 있어서 매우 중요한 역할을 담당한다.
'전공과목 정리 > 이산수학' 카테고리의 다른 글
| [이산수학🔗] 행렬과 행렬식 (10장) (2) | 2023.01.15 |
|---|---|
| [이산수학🔗] 순열, 이산적 확률, 재귀적 관계 (9장) (0) | 2023.01.13 |
| [이산수학🔗] 그래프 (7장) (0) | 2023.01.13 |
| [이산수학🔗] 함수 (6장) (0) | 2023.01.07 |
| [이산수학🔗] 관계 (5장) (2) | 2023.01.07 |